Квадратурная фильтрация

Частотный подход к вейвлет-преобразованиям

Частотный подход и быстрое вейвлет-преобразование

Триумфальный прогресс использования вейвлетов в огромном спектре приложений, связан, в первую очередь, с «быстрыми алгоритмами» (быстрое вейвлет-преобразование – БВП), которые в свою очередь получаются в результате тщательного выбора первичного вейвлета.

Для работы по обработке и представлению реальных сигналов необходимо использовать аппарат частотной фильтрации и методы быстрого вейвлет-преобразования. Они основаны на пирамидальном алгоритме Малла и прореживании спектра по частоте.

Частотная область вейвлетов может быть разбита на две составляющие – низкочастотную и высокочастотную. Их частота раздела равна половине частоты дискретизации сигнала. Для их разделения достаточно использовать два фильтра – низкочастотны Lo и высокочастотный Hi, ко входам которых подключается сигнал s. Фильтр Lo дает частотный образ для аппроксимации (грубого приближения) сигнала, фильтр Hi – для его детализации. Вейвлет коэффициенты соответствуют коэффициентам передаточной характеристики этих фильтров, т.е. коэффициенты фильтров Lo и Hi есть детализирующие коэффициенты вейвлет-декомпозиции сигналов и их коэффициенты аппроксимации.

Поскольку фильтры передают только половину всех частотных компонентов сигнала, то не все попавшие в полосу прозрачности компоненты могут быть удалены. Это называется операцией децимации вдвое и обозначается как ↓2. Если сложить полученные на выходах фильтров сигналы, то получится исходный сигнал, т.е. имеет место полная реконструкция сигнала на начальном уровне реконструкции.

Однако L₀ фильтр можно разложить на два фильтра и подвергнуть спектры этих новых фильтров операции прореживания по частоте – децимации. Это означает изменение уровня реконструкции. Т.е. может быть сформирована система вейвлет-фильтров, реализующих операцию декомпозиции сигнала того или иного уровня.

Подобные операции сокращают спектр соответствующих компонентов сигнала, что лежит в основе приближенного представления сигнала на разных уровнях декомпозиции сигнала. Такое представление необходимо для реализации операций сжатия сигналов и их отчистки от шума. Операция последовательной разбивки L₀ фильтров и постепенного огрубления сигнала была предложена Маллом.

Каждый ортогональный вейвлет имеет свой Фурье-образ ψ(ω), который можно представить реализацией двух фильтров – низкочастотного H (ω) и согласованного с ним высокочастотного фильтра:

G (ω) = 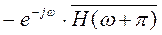. (10)

При этом Фурье-образ вейвлета имеет вид:

ψ(2ω) = G (ω)φ(ω). (11)

Обычно фильтры имеют тип ФНЧ с импульсной характеристикой класса КИХ.

Кратномасштабный анализ основан на двух хорошо известных методах обработки сигналов, заимствованных из теории фильтрации сигналов:

● разложение сигнала по поддиапазонам при помощи квадратурных зеркальных фильтров;

● пирамидальное представление.

Первый метод возник из потребностей обработки звуковых сигналов, а второй - из обработки сигналов изображения.

Пусть имеется некий обобщенный сигнал в виде последовательности чисел 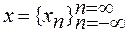. Для сглаживания сигнала, подавления шума часто используют фильтры, базирующиеся на операции свертки:

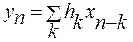. (12)

Сигнал 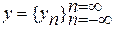получается «локальным усреднением» сигнала x с помощью набора «весов» 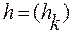. Используя понятия частотного анализа можно записать:

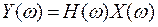, (13)

или что принято в анализе цифровых сигналов, в терминах z-преобразования

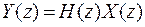. (14)

Транспонированный фильтр h * состоит из тех же коэффициентов, что и фильтр h, но переставленных в обратном порядке. В частотной области транспонированный фильтр записывается как 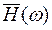. Коэффициенты всех сигналов и фильтров предполагаются вещественными. Величина 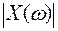характеризует распределение энергии сигнала по частотам .

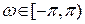Для поставленной задачи находим два фильтра, которые позволили бы разложить сигнал на два частотных компонента – высокочастотны 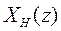и низкочастотный 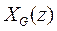, их проредить, затем с помощью транспонированных фильтров, точно восстановить по этим данным исходный сигнал. В случае ограниченного спектра сигнала разумно сделать полосы пропускания фильтров равными половине общей полосы частот спектра сигнала, т.е. граничная частота фильтров должна быть равна половине частоты квантования сигналов.

Пусть теперь вектор Y (z) перед кодированием прореживается вдвое, а перед восстановлением исходного сигнала доводится до исходной длины вставкой нулей между соседними значениями его элементов. При этом z-преобразование из Y (z) превращается в (Y (z)+ Y (- z))/2. Получим z-преобразования компонент перед восстановлением:

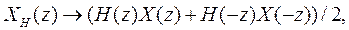
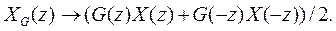
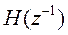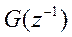z -преобразования транспонированных фильтров имеют вид и .Сигнал восстановится с их помощью точно, если:

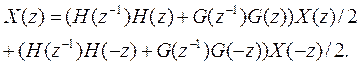
Тогда условия точного восстановления (perfect reconstruction, PR) будут иметь вид:

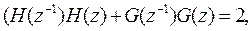
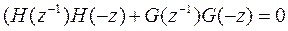
В матричной форме они записываются:

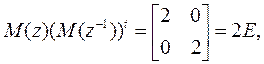
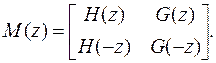
Подставим , получим условия на ДПФ искомых фильтров:

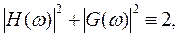(15)

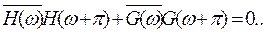(16)

Если

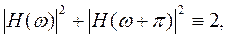(17)

то

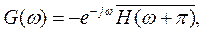(18)

видно, что (15) выполняется.

Фильтры H и G (или L), удовлетворяющие (15) называются квадратурными зеркальными фильтрами – КЗФ. Понятие о них широко используется и в технике вейвлет-преобразований и составляет основу быстрого вейвлет-преобразования (БВП).

Для ряда типов вейвлетов частотное представление открывает возможности использования быстрого вейвлет-преобразования, производя деления спектра на две составляющие и прореживания их по частоте. Его последовательное применение и есть, пирамидальный алгоритм Малла, дающий приближения сигнала с уменьшающейся по мере удаления от вершины дерева детальностью представления сигнала.