Возникновение потенциального барьера. Контактная разность потенциалов

Если в кристалле создать области с электронной и дырочной проводимостью (рис. 5.2) с резкой границей между ними (pn -переход), то на границе между этими областями возникнет потенциальный барьер, обладающий выпрямительными свойствами.

Предположим, что акцепторная область полупроводника легирована сильнее, чем электронная, т.е. N_a>N_d и обе части легированы равномерно (такой pn -переход называется несимметричным и ступенчатым) (рис. 5.2).

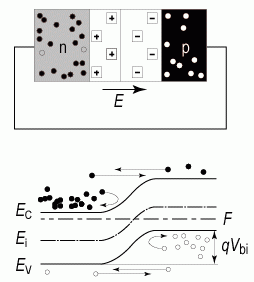
При возникновении pn -перехода между p - и n -областями устанавливается обмен свободными носителями заряда, из материала n -типа выходят (диффундируют) электроны, а из материала p -типа - дырки. Уход свободных носителей приводит к тому, что вблизи границы раздела появляется двойной заряженный слой из ионизованных атомов доноров и акцепторов. Слой объемного пространственного заряда (ОПЗ) будет положительным со стороны материала n- типа (ионизованные доноры) и отрицательным со стороны материала p- типа (ионизованные акцепторы). Эти объемные заряды в области контакта создадут сильное электрическое поле, направленное от n -области к p - области и препятствующее диффузии электронов и дырок (рис. 5.3).

В результате установится равновесное состояние, которое будет характеризоваться постоянством уровня Ферми, а в области перехода, где имеется электрическое поле, энергетические уровни будут искривлены.

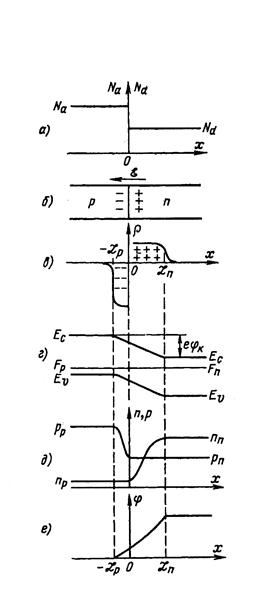Рис. 5.2

При некотором значении поля установится равновесие, при котором количество носителей зарядов переходящих навстречу друг другу одинаково. Этому электрическому полю соответствует равновесное значение контактной разности потенциалов φ_к (рис. 5.2, г).

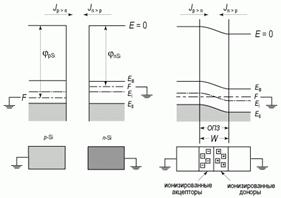Рис. 5.3

Перераспределение носителей, образовавшееся при контакте, и формирование потенциального барьера высотой qφ_к приводит к тому, что диффузионный поток основных носителей (n_n и p_p) прекращается. Энергетический барьер существует именно для основных носителей, потенциального барьера для неосновных носителей (n_p и p_n) нет (см. рис. 5.2,б).

Для того чтобы рассчитать распределения концентраций свободных носителей в приповерхностной области необходимо решить уравнение Пуассона (3.38), устанавливающее связь между распределением потенциала и пространственного заряда ρ (x):

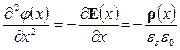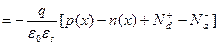(5.3)

Как видно из диаграмм рис 5.2, г величина контактной разности потенциалов равна: .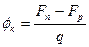

Потенциальный барьер на pn -переходе при термодинамическом равновесии определяется уравнением

.

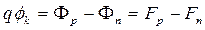(5.4)

Можно показать:

.

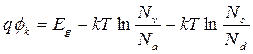(5.5)

Отсюда следует, что максимальная контактная разность потенциалов для невырожденных полупроводников 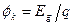. Предполагая, что вся примесь ионизована, 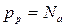, , 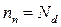а также учитывая, что 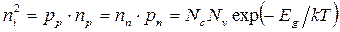, получим:

,

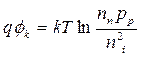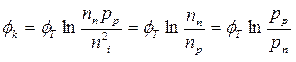(5.6)

где φ_T = kT/q – тепловой потенциал равный 0,026 В при комнатной температуре.

Потенциальный барьер в pn- переходе тем выше, чем сильнее легированы p -и n -области. По мере роста температуры величина n_i² в (5.6) должно возрастать согласно (2.16). Выражение под знаком логарифма стремится к нулю, т.е. контактная разность потенциалов с ростом температуры уменьшается. Этот результат понятен с физической точки зрения. При высоких температурах начинает доминировать собственная проводимость как в p -, так и в n -области, при этом в каждой из областей уровень Ферми стремится к середине запрещенной зоны и qφ_к стремится к нулю.

Из (5.6) можно легко получить:

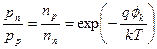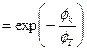(5.7)

Тогда соотношения между основными и неосновными носителями:

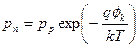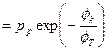.	(5.8)
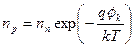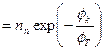.	(5.9)

Уравнения (5.8) и (5.9) можно рассматривать как граничные условия при нулевом внешнем смещении V_см = 0.

Толщина слоя ОПЗ 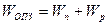. В интервале 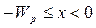объемный заряд отрицательный 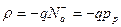. Уравнение Пуассона (5.3) примет вид:

.

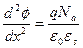(5.10)

В интервале 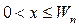объемный заряд положительный 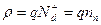и уравнение Пуассона запишется в виде:

.

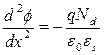(5.11)

Граничные условия:

, .

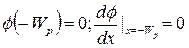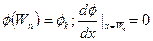(5.12)

Решения уравнений:

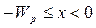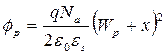при , при.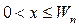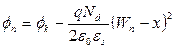

(5.13)

При x=0 потенциал (рис. 5.2, е) и его производные непрерывны, поэтому 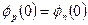; 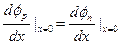. Получаем: 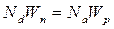. Следовательно, в обеих областях полупроводника, прилегающих к pn- переходу, объемные заряды равны. Это является условием электронейтральности.

Из (5.13) нетрудно получить следующие соотношения:

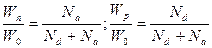.	(5.14)
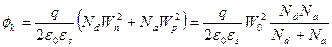.	(5.15)

Отсюда

.

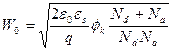(5.16)

Из этой формулы следует, что чем выше степень легирования n- и p-областей полупроводника, тем меньше толщина ОПЗ. Если одна из областей легирована значительно сильнее другой, то большая часть падения потенциала приходится на высокоомную область (рис. 5.2е).