A 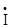 =0; A
=0; A 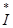 =0
=0
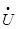 = A т*φ;
= A т*φ; 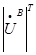 *
*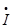 B =φт* A *
B =φт* A *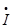 B =0
B =0
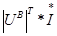 в
в 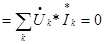
 S̃=
S̃=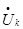 *
*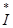 k
k 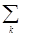 S̃k=0 Сумма комплексных мощностей всех ветвей схемы равна нулю
S̃k=0 Сумма комплексных мощностей всех ветвей схемы равна нулю

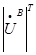 *
* =0 - теорема Теллегена
=0 - теорема Теллегена
Докажем что сумма мощностей отдаваемая источниками равна сумме мощностей потребляемых цепью.
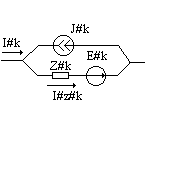
 k=
k= zk-
zk-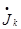
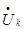 =
=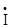 zk*zk-
zk*zk-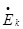
Uk*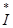 k=Uk*(
k=Uk*(

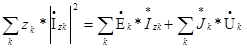
S̃потр. S̃ист.
S̃E =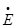
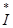 S̃J=
S̃J=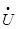
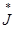
S̃потр=(r+jx)* 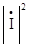 =r*
=r*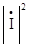 +jx*
+jx*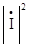 =Pпотр+jQпотр
=Pпотр+jQпотр
S̃ист=Pист+jQист

S̃ист= S̃потр Баланс мощности
Передача мощности от активного двухполюсника к 



 пассивному в цепях синусоидального тока и напряжения.
пассивному в цепях синусоидального тока и напряжения.
 I zвх
I zвх








 U. zн=R+jx
U. zн=R+jx
 A П Ep
A П Ep
 |
Zвх=rвх+jxвх
Zн=rн+jxн
P=zн*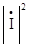 ;
; 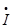 =
=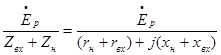
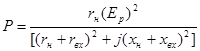
Максимальная мощность:
1) xн= -xвх; 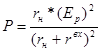
 2) rн=rвх; zн=rвх-jxвх
2) rн=rвх; zн=rвх-jxвх
Пример:
 r
r


 U(t) Y
U(t) Y
 i(t) L
i(t) L
C
U(t)=10*sin(104*t) B
ω=104 рад/с ω=2πf
r=10 Ом; C=0.5*10-5 Ф
i(t), rвх -?
Используем метод комплексных амплитуд:
 U(t) U=
U(t) U=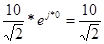
Zвх=r+jωL-j/(ωC)=r+zL+zC
ZL=jωL=10j Ом
ZC= -j/(ωC)= -20j Ом
Zвх=10+10j-20j=10-10j
10 -10j Характер активно-емкостной
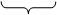 |






 I=U/zвх=
I=U/zвх=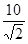
 Четырёхполюсные элементы их матрицы и уравнения.
Четырёхполюсные элементы их матрицы и уравнения.
Схемы трехполюсников, рассмотренные как четырехполюсники
с одним зажимом



|

 1 2
1 2
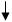 ‘U’1 ‘U’2
‘U’1 ‘U’2
 1’ 2’
1’ 2’
 2014-02-13
2014-02-13 2414
2414
