Расчет линейных электрических цепей переменного тока
Учебно-методическая разработка к выполнению контрольных заданий
Г. Пенза 2005 г.
УДК 621.3.024
Р 24.
Даны методические указания к выполнению расчетно-графических работ по анализу цепей переменного тока.
Работа выполнена на кафедре «Электроника и электротехника» Пензенской государственной технологической академии и предназначена для студентов специальностей 2201, 2102, 1201, 0706, 1706, 3302, 0305.
Ил. 14, табл. 5, библ. назв. 3.
Составители: Ю.А. Смагин, Л.М. Вдовина, Фролов Г.В.
Рецензент: Зав. каф. «ВМиС» ПГТА, процессор Сальников И.И.
Общие методические указания
Расчет линейных цепей переменного тока сводится к расчету токов в ветвях и напряжений на отдельных участках цепи. При одном источнике электрической энергии в схеме основными расчетными уравнениями являются уравнения, составленные на основе законов Ома и Кирхгофа.
Широкое распространение на практике получил метод комплексных амплитуд, использующий алгебру комплексных чисел и позволяющий применять все методы расчетов цепей постоянного тока к цепям переменного тока.
Метод комплексных амплитуд
Метод комплексных амплитуд основан на представлении синусоидальных функций через экспоненты с мнимым аргументом. Аналитически комплексное число можно представить в алгебраической, тригонометрической и показательной форме:
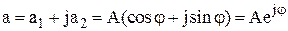 ,
,
где 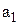 и
и 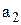 - вещественная и мнимая составляющая,
- вещественная и мнимая составляющая, 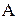 - модуль комплексного числа,
- модуль комплексного числа, 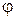 - аргумент комплексного числа.
- аргумент комплексного числа.
Геометрически комплексное число представляется вектором на комплексной плоскости с прямоугольными (рис. 1) или полярными координатами (рис. 2).
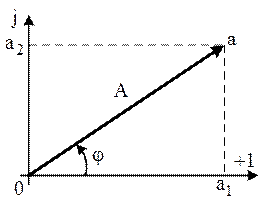 Рис. 1 Рис. 1 |  Рис. 2 Рис. 2 |
Модуль и аргумент комплексного числа можно найти из прямоугольного треугольника (рис. 1):
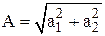 ;
; 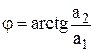 .
.
Разложим по формуле Эйлера выражение 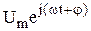 :
:
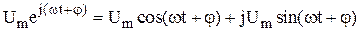 .
.
Мнимая часть этого выражения является синусоидально-изменяющимся напряжением:
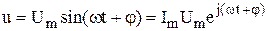 .
.
На плоскости комплексная амплитуда 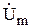 изображается вектором, аргумент которого равен начальной фазе
изображается вектором, аргумент которого равен начальной фазе 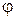 , а длина пропорциональна вещественной амплитуде
, а длина пропорциональна вещественной амплитуде 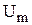 (рис. 3).
(рис. 3).
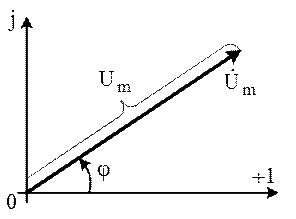 | 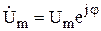 . . |
Рис.3
Комплекс действующего значения равен комплексной амплитуде, деленной на 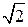 .
.
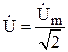 .
.
Комплексное сопротивление 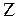 представляет собой отношение комплексных амплитуд напряжения и тока:
представляет собой отношение комплексных амплитуд напряжения и тока:
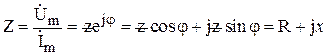 ,
,
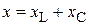 - модуль реактивного сопротивления;
- модуль реактивного сопротивления;
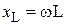 - модуль индуктивного сопротивления;
- модуль индуктивного сопротивления;
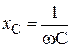 - модуль емкостного сопротивления;
- модуль емкостного сопротивления;
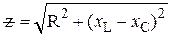 - модуль комплексного сопротивления.
- модуль комплексного сопротивления.
Закон Ома для цепи синусоидального тока запишется в виде: 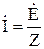 ,
,
где 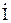 - комплекс действующего значения тока;
- комплекс действующего значения тока;
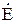 - комплекс действующего значения э.д.с.;
- комплекс действующего значения э.д.с.;
Первый закон Кирхгофа для цепи синусоидального тока записывается, как 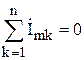 .
.
Алгебраическая сумма комплексных амплитуд токов, сходящихся в узле, равна нулю.
Второй закон Кирхгофа выражается, как
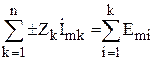 .
.
Алгебраическая сумма комплексных амплитуд падений напряжений на элементах контура равна алгебраической сумме комплексных амплитуд э.д.с. источников этого контура.
В таблице 1 приведены элементы  ,
,  ,
, 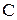 , уравнения для мгновенных значений
, уравнения для мгновенных значений 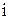 и
и 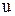 , связь между ними, закон Ома, векторные диаграммы.
, связь между ними, закон Ома, векторные диаграммы.
Таблица 1.
Резисторный  | Индуктивный 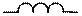 | Емкостной 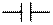 | |
Мгновенные значения 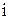 и и 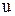 . . | 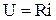 . . | 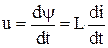 . . | 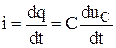 . . |
Связь между 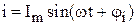 и и 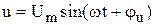 . . | 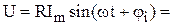 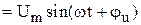 ; ; 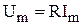 ; ; 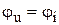 . . | 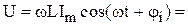 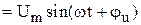 ; ; 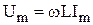 ; ; 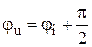 . . | 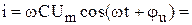 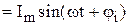 ; ; 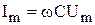 ; ; 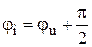 . . |
| Закон Ома в комплексной форме. | 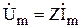 или или 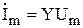 , где , где 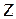 - комплексное сопротивление; - комплексное сопротивление; 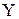 - комплексная проводимость. - комплексная проводимость. | 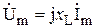 или или 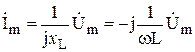 , где , где 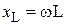 - индуктивное сопротивление. - индуктивное сопротивление. | 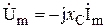 или или 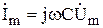 , где , где 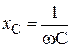 - емкостное сопротивление. - емкостное сопротивление. |
Векторная диаграмма 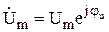 , , 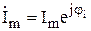 . . | 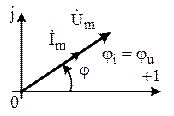 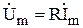 . . | 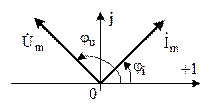 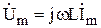 ; ; 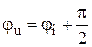 . . | 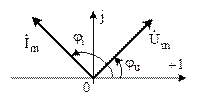  ; ; 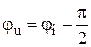 . . |
Правильность расчетов линейных электрических цепей переменного тока проверяется по балансу активной мощности.
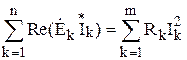 ,
,
где 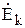 - комплекс действующего значения э.д.с.;
- комплекс действующего значения э.д.с.;
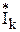 - сопряженный комплекс действующего значения тока, например,
- сопряженный комплекс действующего значения тока, например, 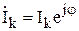 , то
, то  ;
;
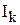 - действующее значение тока в ветви с активным сопротивлением
- действующее значение тока в ветви с активным сопротивлением 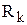 .
.
Мощность в цепи переменного тока можно подсчитать и по действующим значениям тока и напряжения.
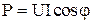 ;
; 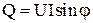 ;
; 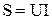 ;
;
где 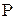 - активная мощность, [Вт];
- активная мощность, [Вт];
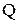 - реактивная мощность, [ВАр];
- реактивная мощность, [ВАр];
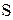 - полная мощность, [ВА];
- полная мощность, [ВА];
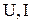 - действующие значения напряжения и тока соответственно;
- действующие значения напряжения и тока соответственно;
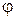 - угол сдвига фаз между напряжением и током,
- угол сдвига фаз между напряжением и током, 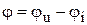 (рис. 4).
(рис. 4).
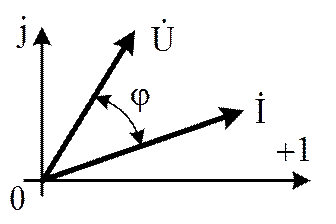
Рис. 4
 2015-05-26
2015-05-26 25087
25087