Теорема о базисном миноре

Строки A = (a ₁,..., a_n), B = (b ₁,..., b_n), C = (c ₁,..., c_n) называются линейно зависимыми, если найдутся такие числа a, b, g, не все равные нулю, что справедливо равенство: aA+bB+gC=0. Но если данное равенство выполняется только тогда, когда все числа a, b, g равны нулю, то строки называются линейно независимыми. Если строки А, В, С линейно зависимы, то, по крайней мере, одну из них можно записать в виде линейной комбинации остальных строк. Пусть a¹0, то A=lB+mC, где l=–b/a, m=–g/a. Все сказанное относится и к столбцам.

Пусть дана матрица А ранга r. По определению ранга эта матрица содержит отличный от нуля минор порядка r. Всякий такой минор называется базисным. Строки и столбцы матрицы, на пересечении которых расположены элементы выбранного базисного минора, называются базисными строками и столбцами.

Теорема 4.1 (о базисном миноре). Любая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов); сами базисные строки (столбцы) линейно независимы.

Пример 4.4. Рассмотрим матрицу

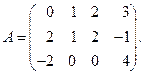
Выберем ненулевой минор 2-го порядка

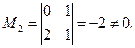
Теперь найдем миноры 3-го порядка, окаймляющие минор M ₂:

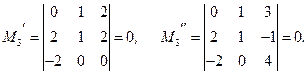
Следовательно, данная матрица имеет ранг Rg A =2, а минор M ₂ будет базисным. Тогда 1-я и 2-я строки:

и 1-й и 2-й столбы:

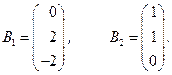
будут базисными. В соответствии с теоремой о базисном миноре все остальные строки и столбцы будут линейной комбинацией базисных строк и столбцов. Например, 3-ю строку

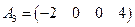
можно представить в виде линейной комбинации базисных строк следующим образом: А ₃ = А ₁– А ₂. à

Следствием теоремы о базисном миноре является

Теорема 4.2. Определитель равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.