Общие положения. Гидромеханика – это наука о движении жидкостей и газов

Гидромеханика – это наука о движении жидкостей и газов. Законы гидромеханики и их практические приложения изучаются в гидравлике, состоящей из двух разделов – гидростатики и гидродинамики. Гидростатика рассматривает законы равновесия и состояние покоя жидкостей и газов. Гидродинамика рассматривает законы движения жидкостей и газов.

В промышленности строительных материалов многие технологические операции связаны с общими законами гидродинамики. Однако изучение этих законов невозможно без рассмотрения некоторых основных понятий гидростатики.

В гидравлике принято объединять жидкости и газы под общим названием – жидкости. Объясняется это тем, что законы движения жидкостей и газов в интервале обычных инженерных расчетов одинаковы.

При выводе основных закономерностей в гидравлике вводят понятие об идеальной жидкости, которая в отличие от реальной (вязкой) жидкости абсолютно несжимаема под действием нагрузки, не изменяет плотности при изменении температуры и не обладает вязкостью. Реальные жидкости подразделяются на капельные (малосжимаемые) и сжимаемые (газообразные). Капельные жидкости незначительно изменяются в объеме при изменении температуры. Плотность их

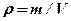где m – масса жидкости; V – ее объем.

Объем упругих жидкостей (газов, паров) сильно изменяется при изменении температуры или давления. Плотность их с большей или меньшей степенью точности может быть рассчитана по уравнению состояния для идеальных газов (уравнению Клапейрона)

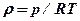где p – давление; R – универсальная газовая постоянная; T – абсолютная температура.

Хотя с позиций физики капельная жидкость значительно отличается от газа, с позиций механики жидкости различие между ними не так велико, и законы, справедливые для капельных жидкостей, могут быть приложены также и к газам, когда сжимаемостью последних можно пренебречь.

Жидкость оказывает давление на дно и стенки сосуда, в котором она находится, и на поверхность любого погруженного в нее тела.

Рассмотрим внутри неподвижной жидкости на некоторой глубине площадку конечных размеров A. Обозначим усилие, с которым жидкость действует на всю эту площадку, через P. Отношение P/A = p_ср называется средним гидростатическим давлением на площадке. Оно представляет собой напряжение, т.е. силу, приходящуюся на единицу площади.

Будем теперь уменьшать площадь А до ∆A и дальше до нуля, одновременно будет уменьшаться и сила Р до ∆P и меньше. Предел, к которому стремится отношение ∆P/∆A, называют напряжением гидростатического давления или просто давлением в данной точке

p = lim (∆P/∆A)

∆A→0

Через каждую точку внутри жидкости может проходить бесчисленное множество элементарных площадок, на которые по нормали действует сила P. Если бы P действовала не по нормали, то ее можно было бы разложить на составляющие – нормальную и параллельную площадке. Последняя вызвала бы перемещение жидкости, что невозможно, так как по условию она находится в состоянии покоя.

Давление в данной точке жидкости не зависит от расположения площадки относительно этой точки и, являясь нормальным к ней, одинаково по всем направлениям, иначе бы также происходило перемещение жидкости внутри занимаемого ею объема.

Все реальные жидкости обладают определенной вязкостью. Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу. Вязкость проявляется в виде внутреннего трения при относительном перемещении смежных частиц жидкости, т.е. вязкость проявляется в жидкостях только при их движении. Если жидкость находится в состоянии покоя, то вязкость отсутствует.

Пусть жидкость течет вдоль плоской стенки параллельными ей слоями (рис. 4.1), как это наблюдается при ламинарном движении. Вследствие тормозящего влияния стенки слои жидкости будут двигаться с разными скоростями, значения которых возрастают по мере удаления от стенки. Рассмотрим два слоя жидкости, движущиеся на расстоянии Δy друг от друга.

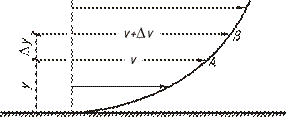
Рисунок 4.1 – Распределение скоростей при течении жидкости вдоль плоской стенки

Слой А движется со скоростью 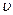, а слой B со скоростью 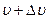. Вследствие разности скоростей слой В за определенную единицу времени сдвигается относительно слоя А на величину 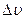. Величина 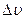является абсолютным сдвигом слоя В по слою А, а отношение 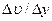, характеризующее относительный сдвиг, есть градиент скорости. Для того чтобы сдвинуть слой В по слою А, к слою В необходимо приложить силу P тем большую, чем больше градиент скорости и площадь соприкосновения F этих слоев. Следовательно, можно записать

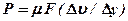где μ – коэффициент пропорциональности.

Возникающая внутри жидкости сила сопротивления R равна приложенной силе P и направлена в противоположную сторону (P = - R). Отношение этой силы к поверхности соприкосновения слоев (F) обозначают буквой τ и называют напряжением сдвига или касательным напряжением (τ = R/F).

Если слои будут находиться бесконечно близко друг к другу, 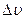и 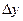можно заменить на 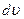и 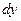и записать

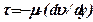(4.1)

Величина μ, характеризующая сопротивляемость жидкости сдвигу, называется динамической вязкостью. Уравнение (1) называют законом внутреннего трения Ньютона, а жидкости, подчиняющиеся этому закону, часто называют ньютоновскими. В технологии строительных материалов чаще приходится иметь дело с неньютоновскими жидкостями, т.е. жидкостями, которые не подчиняются этому закону: литым бетоном, строительными растворами, коллоидными растворами и многими другими.

Иногда вязкость жидкостей характеризуют кинематической вязкостью ν, представляющей собой отношение динамической вязкости жидкости к ее плотности

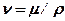Эта вязкость названа кинематической, так как в ее размерности отсутствуют единицы силы или массы. Кинематическая вязкость измеряется в м²/с. Динамическая вязкость имеет размерность Па∙с.

Вода принадлежит к наименее вязким жидкостям. При температуре 20 ⁰С динамическая вязкость воды равна 0,001 Па∙с; кинематическая – 1∙10^-6 м²/с.

Для определения динамической вязкости воздуха применяется формула Милликена:

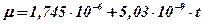что дает μ = 1,82∙10^-5 Па∙с при t = 15 ⁰C. Динамическая вязкость других газов имеет примерно такой же порядок величин. Кинематическая вязкость воздуха для нормальных условий (температура 20 ⁰С, давление р = 101 325 Па = 1 ат) 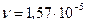м²/с.