Движение молекул газа подчиняется законам статистической физики. В среднем скорости и энергии всех молекул одинаковы. Однако в каждый момент времени энергия и скорости отдельных молекул могут значительно отличаться от среднего значения.
С помощью теории вероятности Максвеллу удалось вывести формулу для относительной частоты, с которой в газе при данной температуре встречаются молекулы со скоростями в определенном интервале значений.
Закон распределения Максвелла определяет относительное число молекул dN/N, скорости которых лежат в интервале (u, u + du).
Оно имеет вид:
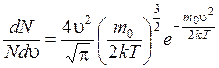 (8.29)
(8.29)
где N – общее число молекул газа;  – число молекул, скорости которых заключены в определенном интервале; u – нижняя граница интервала скоростей; d u – величина интервала скоростей; T – температура газа; e = 2,718… – основание натуральных логарифмов;
– число молекул, скорости которых заключены в определенном интервале; u – нижняя граница интервала скоростей; d u – величина интервала скоростей; T – температура газа; e = 2,718… – основание натуральных логарифмов;
k = 1,38×10-23 Дж/К – постоянная Больцмана; m 0 – масса молекулы.
При получении этой формулы Максвелл основывался на следующих предположениях:
1. Газ состоит из большого числа N одинаковых молекул.
2. Температура газа постоянна.
3. Молекулы газа совершают тепловое хаотическое движение.
4. На газ не действуют силовые поля.
Отметим, что под знаком экспоненты в формуле (8.29) стоит отношение кинетической энергии молекулы 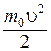 к величине kT, характеризующей среднее (по молекулам) значение этой энергии.
к величине kT, характеризующей среднее (по молекулам) значение этой энергии.
Распределение Максвелла показывает, какая доля dN/N общего числа молекул данного газа обладает скоростью в интервале от u до u + du.
График функций распределения (рис. 8.5) асимметричен. Положение максимума характеризует наиболее часто встречающуюся скорость, которую называют наиболее вероятной скоростью um. Скорости, превышающие um, встречаются чаще, чем меньшие скорости. С повышением температуры максимум распределения сдвигается в направлении больших скоростей.
Одновременно кривая становится более плоской (площадь, заключенная под кривой, не может измениться, так как число молекул N остается постоянным).
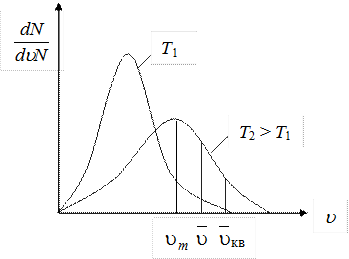
Рис. 8.5
Для определения наиболее вероятной скорости нужно исследовать на максимум функцию распределения Максвелла (приравнять первую производную к нулю и решить относительно u). В результате получаем:
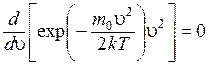 .
.
Мы опустили множители, не зависящие от u. Осуществив дифференцирование, придем к уравнению:
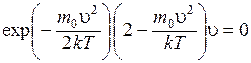 .
.
Первый сомножитель (экспонента) обращается в нуль при u = ¥, а третий сомножитель (u) при u = 0. Однако из графика (рис. 8.5) видно, что значения u = 0 и u = ¥ соответствуют минимумам функции (8.29). Следовательно, значение u, отвечающее максимуму, получается из равенства нулю второй скобки: 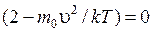 . Отсюда
. Отсюда
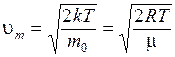 . (8.30)
. (8.30)
Введем обозначения для функции распределения молекул по скоростям (8.29):
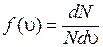 . (8.31)
. (8.31)
Известно, что среднее значение некоторой физической величины j(x) можно вычислить по формуле:
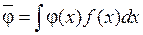 . (8.32)
. (8.32)
Из (8.32) получим выражения для среднего значения модуля скорости u и среднего значения квадрата u:
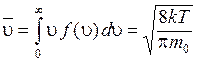 , (8.33)
, (8.33)
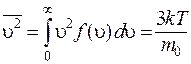 . (8.34)
. (8.34)
Таким образом, средняя скорость молекул (ее называют также средней арифметической скоростью) имеет значение:
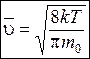 . (8.35)
. (8.35)
Квадратный корень из выражения (8.34) дает среднюю квадратичную скорость молекул:
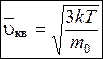 . (8.36)
. (8.36)
Отметим, что она совпадает с формулой (8.24). На рис. 8.5 приведен график функции распределения Максвелла. Вертикальными линиями отмечены три характерные скорости 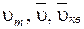 .
.
 2014-02-24
2014-02-24 25065
25065
