Рассмотрим установившийся ламинарный поток жидкости в прямой трубе круглого сечения радиусом R. Как известно, ламинарное движение имеет слоистый характер и происходит без перемешивания частиц. Один слой движется по другому, причем между ними возникает сила трения, напряжение которой определяется законом внутреннего трения Ньютона
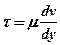 ;
;
где ν – местная скорость движения (скорость в рассматриваемой точке).
Разобьем поток жидкости на ряд кольцевых слоев, соосных с трубой. Пусть у стенок трубы скорость частиц жидкости, соприкасающихся с нею, равна нулю вследствие наличия силы трения по величине большей, чем движущая сила, которой является разность давлений. Выделим в потоке цилиндрический слой радиусом r, длиной l и толщиной dr (рис. 4.8).
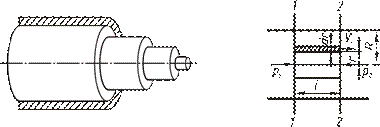
Рисунок 4.8 – К определению расхода жидкости в ламинарном потоке
Движущая сила равна разности сил давлений P1 и P2, которая определяется площадью живого сечения потока и гидростатическим давлением p1 и p2 в сечениях 1-1 и 2-2:
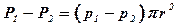 .
.
Движению цилиндра оказывает сопротивление сила трения:
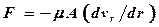 ,
,
где νr – скорость движения цилиндра; r – расстояние от оси до образующей цилиндра; 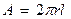 – наружная поверхность цилиндра; μ – вязкость жидкости.
– наружная поверхность цилиндра; μ – вязкость жидкости.
При установившемся движении:
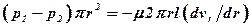 .
.
После преобразования и разделения переменных получим
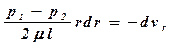 .
.
Интегрируя это выражение для всего объема жидкости при изменении r до R и νr до 0, получим
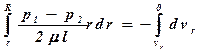 .
.
Решая, получим
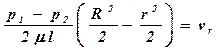 или
или 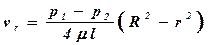 . (4.24)
. (4.24)
Очевидно, что максимальное значение скорости будет при r = 0
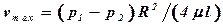 . (4.25)
. (4.25)
Разделив (4.24) на (4.25), получим
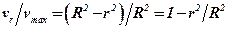 ,
,
откуда
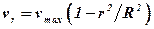 . (4.26)
. (4.26)
Следовательно, при ламинарном движении распределение скоростей в трубе параболическое. Уравнение (4.26) представляет собой закон Стокса. Площадь кольцевого сечения dA с внутренним радиусом r и внешним r+dr равна 2πrdr. Тогда объемный расход жидкости через это сечение составит
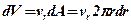 . (4.27)
. (4.27)
Подставляя значения vr из уравнения (1), получим
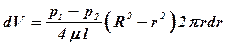 .
.
Общий расход жидкости через все сечение получим интегрированием последнего выражения:
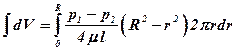
или 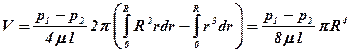 . (4.28)
. (4.28)
Обозначая (p1 – p2) = ∆ p и d = 2R, получим уравнение Пуазейля для расхода жидкости при ламинарном движении по круглой трубе:
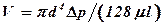 . (4.29)
. (4.29)
Сравнивая формулу для объемного расхода жидкости
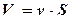 ,
,
где v – средняя скорость потока; S – площадь живого сечения потока, с формулой (4.28), можно получить выражение для средней скорости потока:
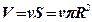 и
и 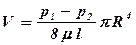 или
или 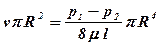 ,
,
откуда 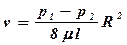 . (4.30)
. (4.30)
Разделив (4.30) на (4.25), получим
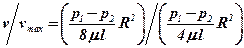 ,
,
откуда 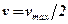 . (4.31)
. (4.31)
Таким образом, при ламинарном движении жидкости в прямолинейной круглой трубе средняя скорость жидкости равна половине скорости по оси трубы.
Подставляя в выражение (4.26) значение vmax из (4.31), получим
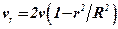 . (4.32)
. (4.32)
Опыт показывает, что средняя скорость турбулентного потока значительно больше половины максимальной, причем их отношение
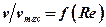 .
.
Например, при Re = 104 средняя скорость 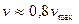 , а при Re = 108
, а при Re = 108 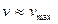 .
.
 2014-02-13
2014-02-13 2047
2047
