Задачи нелинейного программирования. Теорема Куна-Таккера

При оптимальном поведении экономической системе или фирме безразлично, использовать ли ресурсы для производства и продать продукты, чтобы получить прибыль или(!!!!!!!) продать ресурсы по эффективным ценам, уже не производя продукты.

Максимизации прибыли.

Наименьшая стоимость набора ресурсов, дающая возможность

Двойственные оценки помогают ответить на вопрос, какова

Максимальной эффективности использования технологий отвечает наилучшая оценка используемых ресурсов.

Максимальная прибыль задачи сопровождается наилучшей оценкой использования ресурсов или

обращения ресурсов в продукты и продажи этих продуктов с целью

Вторая теорема двойственности. Для того чтобы пара планов x*, y* была оптимальной в прямой и двойственной задачах соответственно, необходимо и достаточно, чтобы выполнялись следующие условия:

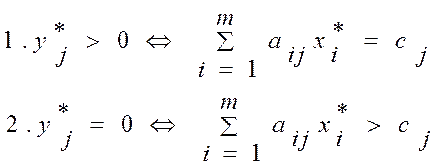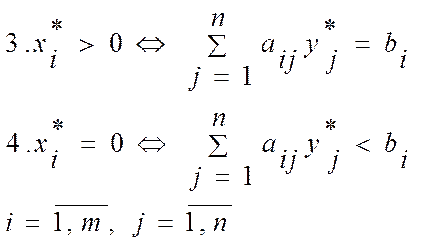Экономический смысл второй теоремы двойственности:

1. Если yj >0, т.е. j-ая технология рентабельна (соответственно, j ограничение двойственной задачи, которое характеризует условные удельные оценки затрат ресурсов при выпуске одной единицы продукции j-го вида, выполняется как строгое равенство), то. условная удельная оценка всех используемых ресурсов при производстве одной единицы продукции j-го вида равна прибыли c_j и наоборот, если условная оценка удельных затрат используемых ресурсов равна прибыли c_j, то данная технология рентабельна.

2. Если yj =0, т.е. j-ая технология нерентабельна, тo

условная удельная оценка затрат больше удельной

прибыли. И наоборот, если условная удельная

оценка затрат ресурсов больше удельной прибыли,

технология нерентабельна.

3. Если xi >0 (условная цена i-го ресурса отлична от 0), то весь i-й ресурс расходуется полностью. Наоборот, если (i-й ресурс используется полностью), то у него есть ненулевая «цена», как мера его дефицитности. Эти «цены» в сравнении с собой устанавливают некоторую упорядоченность среди дефицитных ресурсов (чем больше «цена», тем более дефицитен ресурс).

4. Если цена равна 0, т.е. i-ый ресурс недефицитен, тогда соответствующее ограничение по расходу i-го ресурса выполняется как строгое неравенство.

Третья теорема двойственности. Если двойственная оценка xi*>0, то вдоль оптимального плана y* эта оценка xi* есть частная производная функции L по i-му аргументу, т.е.

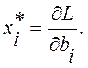Третью теорему двойственности можно использовать для приближенного определения изменения прибыли в исходной задаче при изменении дефицитных ресурсов без решения новой задачи с измененными ресурсами.

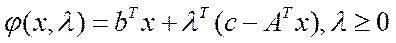Введем функцию Лагранжа для (1)

Из второй теоремы двойственности следует, что на оптимальном решении задач (1),(2) существует такое

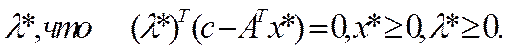
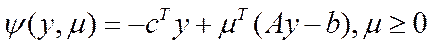Образуем функцию Лагранжа в задаче (2)

Опять же на оптимальном решении задач (1),(2) существует такое

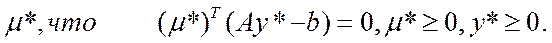
Если положить .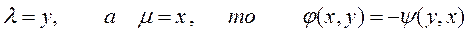

Используя функции Лагранжа 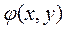и 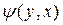можно показать(!!!!!), что задача (1) может быть записана в виде

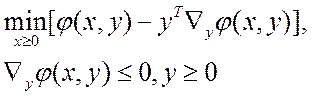
А задача (2)

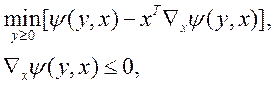
Учитывая 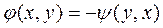имеем следующее представление для задачи (2)

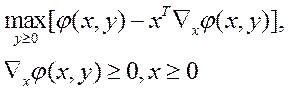
Из второй теоремы двойственности следует, что на оптимальном решении x*, y*,

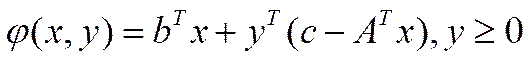Оказывается, что для введенной здесь функции Лагранжа

имеется очень интересное свойство

Теорема. Неотрицательный вектор х* является оптимальным решением задачи (1) т.т.т.к. существует неотрицательный вектор у*,что пара (х*,у*) является седловой точкой функции Лагранжа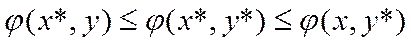

Или

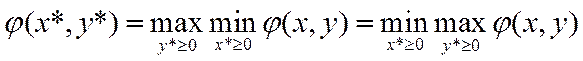
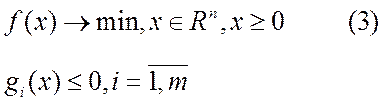
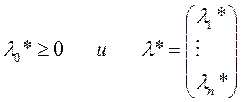Теорема Куна-Таккера. В задаче (3) х* есть точка локального минимума, если существуют

одновременно не равные нулю и такие, что

,

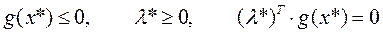и если при этом градиенты активных ограничений в точке х* линейно независимы (условие регулярности), то .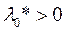

Теорема Вулфа. С помощью функций Лагранжа в задаче нелинейного программирования по аналогии с задачами ЛП Вулфом была доказана следующая

Теорема. Пусть функция 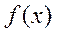и все функции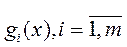

выпуклые и дифференцируемые, а также выполняются условие Слейтера. Тогда задача (3) может быть записана как

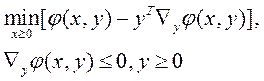
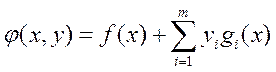где

Если задача (3) имеет решение х*, то в двойственной задаче

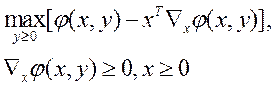
существует такое y*, что (х*,у*) является решением двойственной задачи, и при этом экстремумы двух задач равны между собой.

Такой результат позволяет и для задач нелинейной оптимизации вводить аналог качественных характеристик – например, двойственные оценки есть мера чувствительности ограничений к изменению параметров (весов, объемов и др.), или условные цены или некие предельные характеристики решения.

Пусть теперь

,

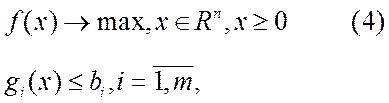где, например, 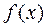означает доход от выпуска х, 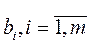- запасы i-го ресурса. Тогда оптимальный множитель Лагранжа 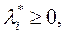для которого выполняется условие дополняющей «нежесткости» 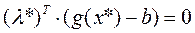, определяет прирост максимального дохода при изменении запаса i-го ресурса на некую малую величину, т.е. .

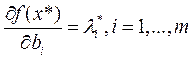Также 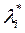есть предельная цена ресурса, которую фирма готова заплатить за безубыточное использование i - го ресурса.