Задачи на условный экстремум функционала с дополнительными ограничениями на переменной
Глава III
Принцип максимума, разработанный группой советских математиков под руководством академика Л.С. Понтрягина, является расширением классического вариационного исчисления на случай, когда на переменную наложены дополнительные ограничения, вследствие чего управляющие воздействия могут иметь на отрезке  разрывы первого рода в конечном числе точек, т.е. описываются кусочно-непрерывными функциями.
разрывы первого рода в конечном числе точек, т.е. описываются кусочно-непрерывными функциями.
Итак, вспомним постановку 6 типовой задачи управления. Дан функционал
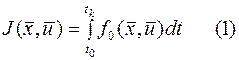 где
где
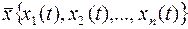 вектор коор. сост.
вектор коор. сост.
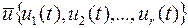 вектор управления
вектор управления
Известны граничные условия

Управление связи, является матиматическим описанием объекта управления
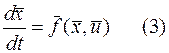
и допустимые ограничения на переменной
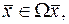
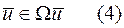
Требуется найти такой вектор управления 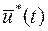 , подгоняющийся (4) и (3), которому бы соответствовала экстремаль
, подгоняющийся (4) и (3), которому бы соответствовала экстремаль 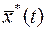 , проходящая через граничные точки (2) и доставляющая экстремум
, проходящая через граничные точки (2) и доставляющая экстремум 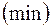 функционалу.
функционалу.
Для того, чтобы геометрически интерпретировать задачу на условный 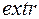 функционалу, введем новую переменную
функционалу, введем новую переменную 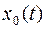 следующим образом
следующим образом
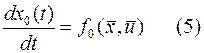
Следовательно
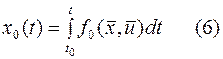 а при
а при 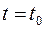
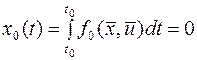 а при
а при 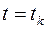
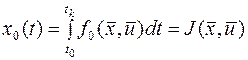
Присоединив 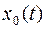 к
к 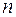 - мерному вектору состояния
- мерному вектору состояния 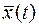 , получим расширенную
, получим расширенную 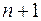 мерную систему координат состояния
мерную систему координат состояния 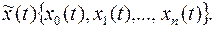 Присоединив же (5) к (3), получим расширенную систему управлений связи
Присоединив же (5) к (3), получим расширенную систему управлений связи
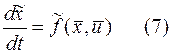
Итак, простая черта над переменной в дальнейшем будет служить признаком 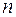 - мерного пространства, волнистая черта – признаком (n+1) мерного пространства. Отметим так же,
- мерного пространства, волнистая черта – признаком (n+1) мерного пространства. Отметим так же, 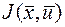 не зависит от вновь введенной переменной
не зависит от вновь введенной переменной 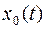 .
.
Предположим, что вектор 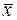 содержит две переменные
содержит две переменные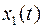 и
и 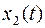 , тогда вектор
, тогда вектор 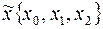 будет соответствовать точка в трехмерном пространстве рис.1
будет соответствовать точка в трехмерном пространстве рис.1
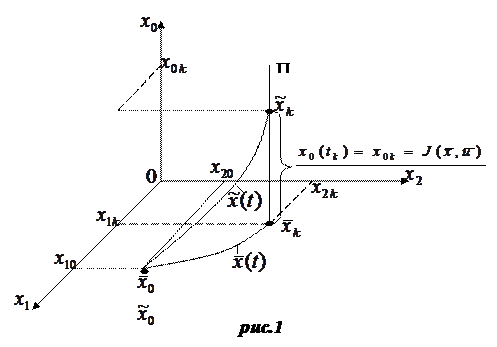
Обозначим через П прямую в пространстве 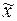 , проходящую через точку
, проходящую через точку 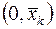 , параллельную оси
, параллельную оси 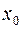 . Кривая
. Кривая 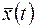 , лежащая в плоскости
, лежащая в плоскости 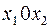 - допустимое решение задачи на условный экстремум функционала. Она является проекцией на плоскости
- допустимое решение задачи на условный экстремум функционала. Она является проекцией на плоскости 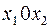 , кривой
, кривой 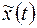 , координата
, координата 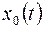 которая в любой момент времени определяется (6).
которая в любой момент времени определяется (6).
Основную задачу оптимального управления можно сформулировать следующим образом.
В (n+1) мерном пространстве 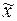 заданы начальная точка
заданы начальная точка 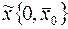 и прямая П, параллельная оси
и прямая П, параллельная оси 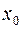 и проходящая через точку
и проходящая через точку 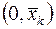 ; среди всех допустимых уравнений обладающих тем свойством, что соответствующее решение системы (7) с начальным условием
; среди всех допустимых уравнений обладающих тем свойством, что соответствующее решение системы (7) с начальным условием 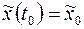 проходит при
проходит при 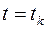 через точку
через точку 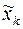 прямой П, выбрать такое управление, для которого координата
прямой П, выбрать такое управление, для которого координата 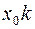 точки
точки 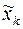 имела бы минимум значения.
имела бы минимум значения.
Напомним, что это была геометрическая постановка задачи на условный 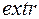 функционала.
функционала.
Перейдем к формулировке теоремы дающей необходимое условие 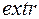 . Введем в рассмотрение вспомогательные переменные
. Введем в рассмотрение вспомогательные переменные 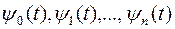 , удовлетворяющие системе уравнений
, удовлетворяющие системе уравнений
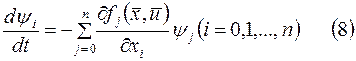
Система уравнений (8) называется сопряженной по отношению к системе (7). Системы уравнений (7) и (8) можно объединить одной формой записи. Для этого введем в рассмотрение функцию 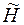 переменных
переменных 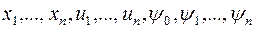 , называемую «Гамильтонианом»
, называемую «Гамильтонианом»
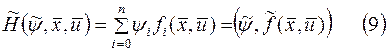
Тогда системы уравнений (7) и (8) можно записать в виде:
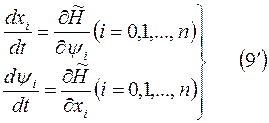 Уравнения Гамильтона
Уравнения Гамильтона
При фиксированных значениях 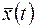 и
и 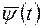 функция
функция 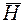 становится только функцией управления
становится только функцией управления 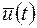 . Обозначим
. Обозначим
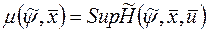 , причем
, причем 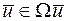
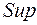 - супремум - это верхняя граница функции
- супремум - это верхняя граница функции 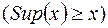 .
.
Если точная верхняя грань достигается, то
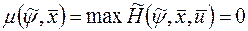 ,
, 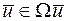
 2014-02-13
2014-02-13 1318
1318








