Пусть 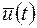
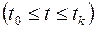
 такое допустимое управление, что соответствующая ему траектория
такое допустимое управление, что соответствующая ему траектория 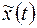 рис.1, исходящая при
рис.1, исходящая при 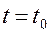 из точки
из точки 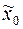 , проходит в момент времени
, проходит в момент времени 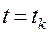 через некоторую точку прямой П. Для оптимальности управления
через некоторую точку прямой П. Для оптимальности управления 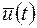 и траектории
и траектории 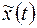 необходимо существование такой не нулевой непрерывной вектор функции
необходимо существование такой не нулевой непрерывной вектор функции 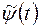 , соответствующей функциям
, соответствующей функциям 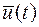 и
и 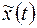 , что
, что
1. При любом 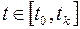 гамильтониан
гамильтониан 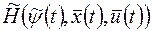 достигает максимума по
достигает максимума по 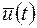 т.е.
т.е.
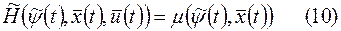
2. В конечный момент имеет место соотношение
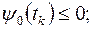
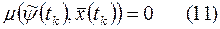
Замечание 1. Доказано, что на интервале 
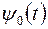 и
и 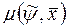 являются константами, поэтому если условия
являются константами, поэтому если условия 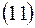 выполняется для
выполняется для 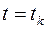 , то они выполняются для любых
, то они выполняются для любых 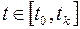 .
.
Замечание 2. В большинстве случаев 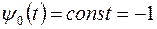 (см. рис. (*))
(см. рис. (*))
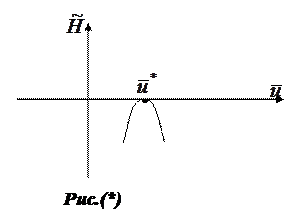
Замечание 3. Теорема получила название принципа максимума в связи с тем, что оптимальное управление 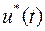 , доставляющие максимум гамильтониану
, доставляющие максимум гамильтониану 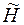 .
.
Следовательно, данная теорема говорит только о необходимости существования функции 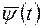 и выполнения условия максимума.
и выполнения условия максимума. 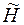 вдоль оптимальной траектории, ноне дает конкретных рекомендаций по выбору оптимального управления.
вдоль оптимальной траектории, ноне дает конкретных рекомендаций по выбору оптимального управления.
* ищется как управление,
Пример. (глава II)
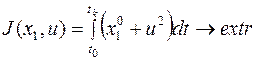
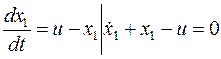
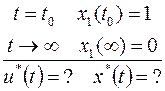
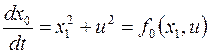
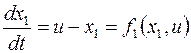
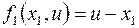
Введем вектор
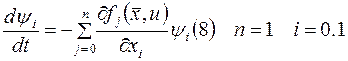
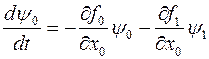 для
для 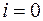
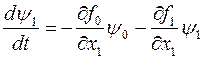 для
для 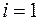
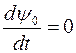 т.к.
т.к. 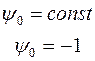 т.е. для задач автоматического управления.
т.е. для задач автоматического управления.
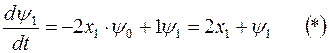
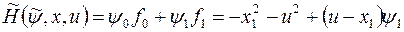 исходя их
исходя их 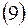
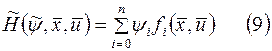
Находим 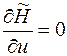 т.е.
т.е. 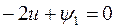
Перепишем варьирование 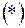
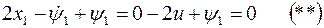
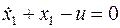 Получили 3 уравнения с 3-мя неизвестными
Получили 3 уравнения с 3-мя неизвестными
Из главы (2) 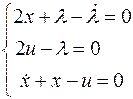
Вектор 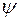 характеризует положение гиперплоскости, т.е. играет так же роль, что и
характеризует положение гиперплоскости, т.е. играет так же роль, что и 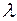 . Следовательно, решение то же самое.
. Следовательно, решение то же самое.
Будем приближенно находить оптимальное управление и оптимальную траекторию.
Начальное 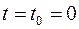 . Найдем значение оптимального управления.
. Найдем значение оптимального управления.
Зададимся 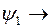 произвольно,
произвольно, 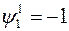
Тогда 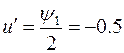 Вычислим
Вычислим 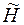
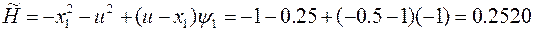 , а должно быть =0
, а должно быть =0
Возьмем 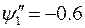
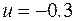
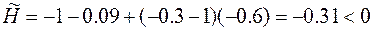
Возьмем 
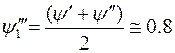
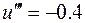
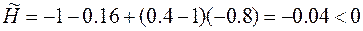
Если точность устраивает, то итерацию можем закончить.
Введем шаг дискретности по времени  ∆
∆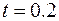
Каждый раз начало отчета берем в новой точке 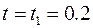 из уравнения
из уравнения
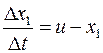 откуда
откуда 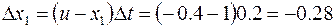
Тогда координата 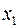 в
в 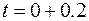 будет
будет 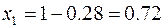
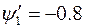
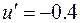
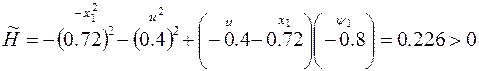
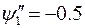
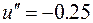
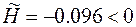
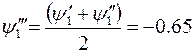
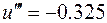
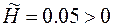
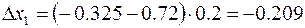
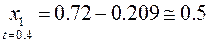 и т.д. см. рис. 1
и т.д. см. рис. 1
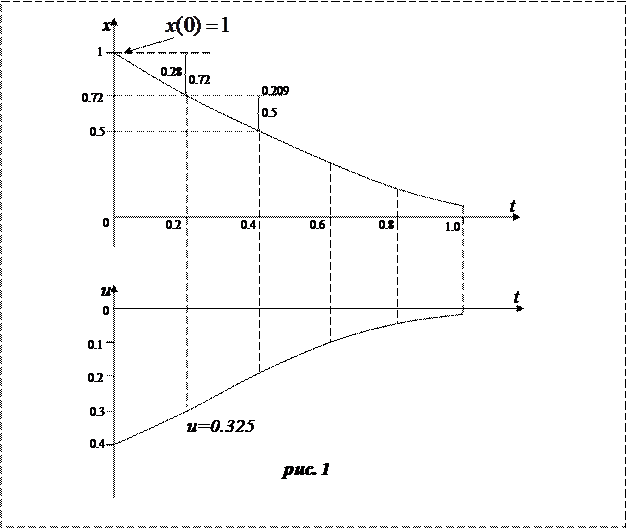
Пример.
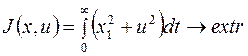
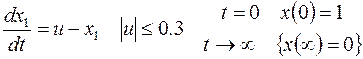
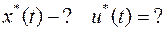

На управление наложено ограничение 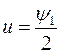
Возможно 2 случая
1) 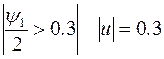
2) 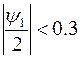 То решение происходит предыдущим способом без ограничений.
То решение происходит предыдущим способом без ограничений.
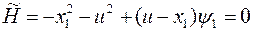 при оптимальном управлении
при оптимальном управлении
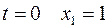 согласно ограниченным условиям определим значение управляющего сигнала при
согласно ограниченным условиям определим значение управляющего сигнала при 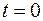 .
.
Замечено, что в начальный момент времени управление берется максимальным.
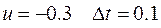
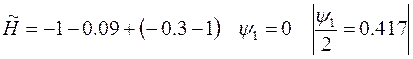
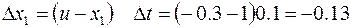
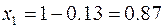
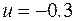
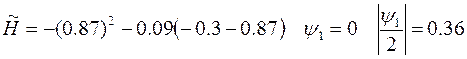
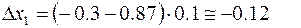
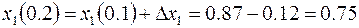
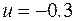
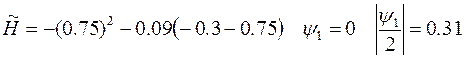
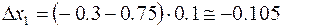
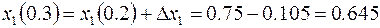
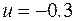
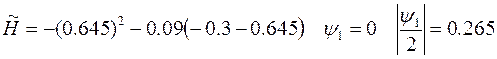
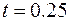
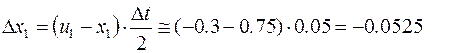
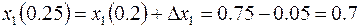
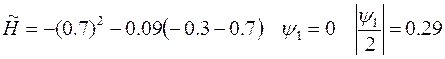
и далее, как в предыдущем примере см. рис. 2
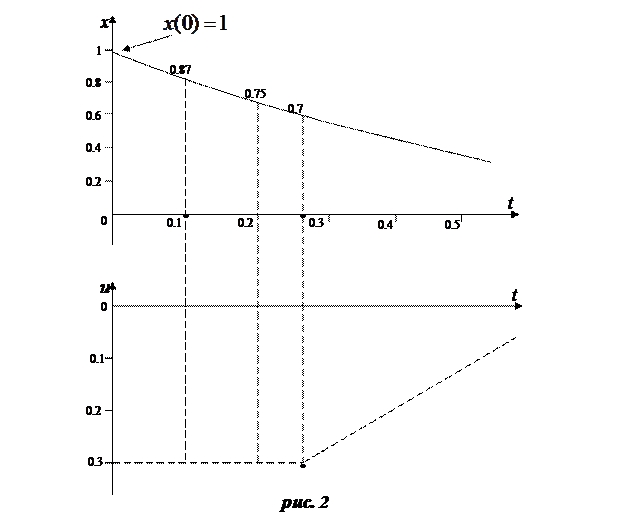
 2014-02-13
2014-02-13 515
515








