В действительности часто силы бывают приложены к какой-либо части объема тела или его поверхности, а иногда к некоторой части линии. Поэтому нужно рассмотреть способы перехода от распределенных сил к сосредоточенным в простейших случаях.
Интенсивность q распределенной силы – это сила, приходящаяся на единицу объема, поверхности или длины линии. Чаще встречаются параллельные и сходящиеся распределенные силы.
Рассмотрим линейные распределенные силы (по линии) на отрезке.
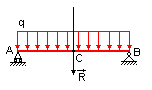
| а) АВ= l 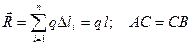
|
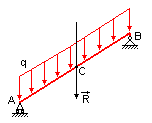
| б) 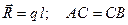 , но , но 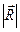 уже не равна площади параллелограмма уже не равна площади параллелограмма
|
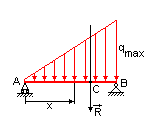
| в) АВ= l; 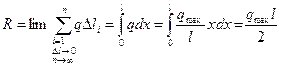 Точку приложения равнодействующей вычислим через определение
момента элементарных сосредоточенных сил
Точку приложения равнодействующей вычислим через определение
момента элементарных сосредоточенных сил
|
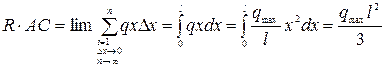
А так как 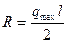 , то
, то 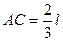 , то есть равнодействующая проходит через центр масс эпюры распределенных сил.
, то есть равнодействующая проходит через центр масс эпюры распределенных сил.
Лекция 4 (статика)
«Силы трения, центр масс»
Силы трения.
А) Трение скольжения
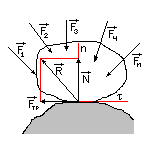
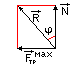
| Тело находится в равновесии под действием системы сил F1,F2,…Fn, а также в контакте с шероховатой поверхностью. Если силу реакции R шероховатой поверхности разложить на составляющие, одна из которых направлена по общей нормали к поверхности соприкосновения – N, а другая находится в касательной плоскости к этим поверхностям – Fтр, то N называется нормальной реакцией, а Fтр –силой трения скольжения. |
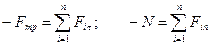
|
|
|
Законы Кулона для сухого трения скольжения
(сформулированы в 1781г., законы приближенные)
1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного или реального скольжения под действием приложенных сил. Сила трения при покое зависит от активных сил и ее модуль меньше максимально возможного значения, которое достигается в момент выхода тела из положения равновесия.
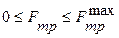
2. Максимальная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей.
3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции)
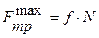
коэффициент трения скольжения f не зависит от нормального давления N
4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей.
Законы трения скольжения справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов трущихся поверхностей.
| Примерные значения коэффициента трения | Для большинства материалов с началом скольжения максимальная сила трения слегка уменьшается с ростом скорости. |
| кирпич-бетон 0.76 сталь-сталь 0.15 дуб-дуб (поперек волокон) 0.54 дуб-дуб (вдоль волокон) 0.62 |
При наличии смазки сила трения существенно зависит от скорости перемещения.
|
|
|
Угол и конус трения.
При равновесии твердого тела под действием активных сил на шероховатой поверхности в предельном состоянии равновесия реакция R отклонена от нормали общей касательной на наибольший угол. Этот угол называют углом трения.
| 
|
Конусом трения называют конус, описанный полной реакцией, построенной на максимальной силе трения, вокруг направления нормальной реакции. Его можно построить изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся поверхностей. Это не обязательно круговой конус (ворс, направление волокон…). Тело нельзя вывести из равновесия любой по модулю активной силой, если ее линия действия проходит внутри конуса трения.
Б) Трение качения
Физическую природу трения качения можно объяснить следующим образом: реальные материалы поверхности и катка испытывают деформацию, поэтому при качении катка по поверхности необходимо как бы «гнать волну деформации» перед катком. Другое объяснение может выглядеть так: при качении катка за счет деформации поверхности нам все время приходится как бы «выкатывать» каток из небольшого углубления.
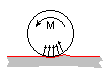
| В любом случае это связано с тем, что при качении катка возникает некомпенсированный момент распределенных сил в области контакта катка и поверхности. Этот момент сил «препятствует» качению и явление, связанное с этими процессами называется трением качения. |
Законы Кулона для трения качения
1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента Mmax пропорционально нормальному давлению:
Mmax = dN, где d - коэффициент трения качения, имеющий размерность [м]
3. Коэффициент d зависит от материала катка, поверхности и их физического состояния и не зависит (в первом приближении) от угловой скорости качения w. Пример: для пары сталь-сталь d=0,5 мм.
Законы трения качения являются приближенными и, как и законы трения скольжения, справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов катка и поверхности.
Разделив момент сопротивления качению на радиус катка можно формально ввести силу трения качения и считать ее приложенной к центру катка, направление противоположно направлению движения.
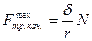 , (r - радиус катка)
, (r - радиус катка)
Обычно d/r << f и для начала качения требуется значительно меньшая сила, чем для скольжения.
Центр масс.
Центром масс механической системы называется точка G(xm,ym,zm) с координатими:
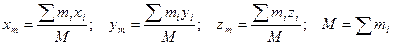
где суммирование производится по всем точкам системы.
Разбивая слагаемые в вышеприведенных формулах на части и проводя выделение и перегруппировку можно показать, что центр масс системы есть центр масс для центров масс ее частей.
Для сплошных тел суммы переходят в интегралы:
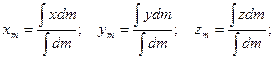
Во всех формулах размерность массы сокращается. Таким образом, можно использовать в качестве массы любую пропорциональную ей величину: объем – для однородных объемных тел, площадь – для однородных плоских фигур, длину – для однородных линейных конструкций.
Методы определения центров масс.
а) метод разбиения на части
 Некоторые тела сложной формы можно разбить на части, положение центра масс которых известно или может быть предварительно определено. Тогда используем общие формулы, только вместо элементарных частиц тела берутся конечные части, на которые оно разбито.
Некоторые тела сложной формы можно разбить на части, положение центра масс которых известно или может быть предварительно определено. Тогда используем общие формулы, только вместо элементарных частиц тела берутся конечные части, на которые оно разбито.
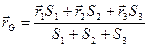
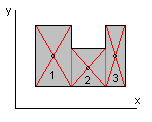
б) метод отрицательных масс
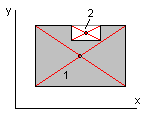 В тех случаях, когда фигуру, положение центра масс которой мы хотим определить, можно дополнить до фигуры, положение центра масс которой хорошо известно, можно использовать метод «отрицательных» масс. В примере прямоугольник с вырезом представляется в виде разности большого (1) и малого (2) прямоугольников. Используем прежние формулы с условием, что масса вырезаемой части считается отрицательной. Этот метод особенно удобен при вычислении положения центров масс тел, имеющих отверстия. Для тел сложной формы можно использовать комбинацию методов а) и б).
В тех случаях, когда фигуру, положение центра масс которой мы хотим определить, можно дополнить до фигуры, положение центра масс которой хорошо известно, можно использовать метод «отрицательных» масс. В примере прямоугольник с вырезом представляется в виде разности большого (1) и малого (2) прямоугольников. Используем прежние формулы с условием, что масса вырезаемой части считается отрицательной. Этот метод особенно удобен при вычислении положения центров масс тел, имеющих отверстия. Для тел сложной формы можно использовать комбинацию методов а) и б).
|
|
|
Для некоторых простых фигур и тел приведем результаты без вывода (часто они понятны даже с точки зрения здравого смысла).
1. Центр масс однородного прямолинейного отрезка лежит в середине отрезка.
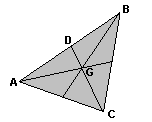
2. Центр масс треугольника лежит в точке пересечения медиан. Медианы в точке пересечения делят друг друга в отношении 2:1 (CG=2 GD)
В тех случаях, когда форма фигуры или тела, положение центра масс которых необходимо определить, являются достаточно сложными, можно применить метод прямого интегрирования. При этом используем интегральные определения, приведенные в начале параграфа.
Рассмотрим дугу окружности радиуса R с углом раствора 2a0.
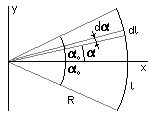 Выделим бесконечно малый элемент дуги dl с углом раствора da и текущим углом a. Длина этого элемента равна dl = Rda, его координата x=RCosa.. Определим положение центра масс дуги по оси x:
Выделим бесконечно малый элемент дуги dl с углом раствора da и текущим углом a. Длина этого элемента равна dl = Rda, его координата x=RCosa.. Определим положение центра масс дуги по оси x:
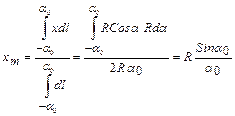
Этот результат при a0=p/2 дает нам формулу для полуокружности, полученную ранее.
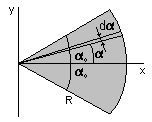
Рассмотрим круговой сектор радиуса R с углом раствора 2a0. Расположим его симметрично оси x, как показано на рисунке. Выделим бесконечно малый сектор с углом раствора da и текущим углом a. В пределе бесконечно малых он представляет собой треугольник высотой R и основанием dl=Rda. Площадь этого треугольника равна dS = (1/2)R2da. Центр масс треугольника лежит в точке пересечения медиан. Таким образом, в проекции на ось x координата положения центра масс треугольника имеет значение x = (2/3)RCosa. Используя определение положения центра масс по оси x, будем иметь:
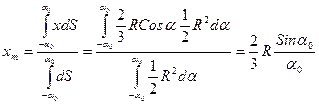
Лекция 5 (кинематика)
«Кинематика точки, скорость и ускорение точки в различных системах координат»
Часть II Кинематика
|
|
|
Кинематика точки (неподвижная система координат).
Скорость и ускорение точки в декартовых координатах
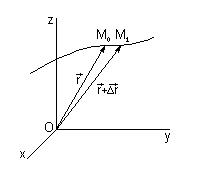
Положение точки М0 определяем радиус-вектором 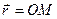 . Если точка движется относительно системы отсчета Oxyz, то ее координаты будут функциями времени
. Если точка движется относительно системы отсчета Oxyz, то ее координаты будут функциями времени
| 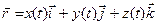
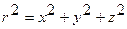 Скорость и ускорение точки М в некоторый момент времени:
Скорость и ускорение точки М в некоторый момент времени:
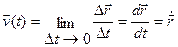
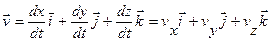
|
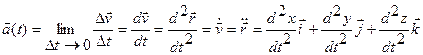
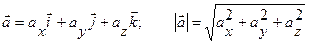
Обозначим через S длину дуги траектории, отсчитываемой с соответствующим знаком от первоначального положения точки на траектории:
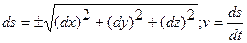
Тогда, очевидно, 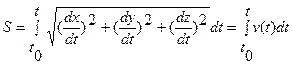
Годограф. К началу неподвижной системы координат О приложим вектор ОР, равный по величине и направлению скорости движущейся точки. При движении точки М по ее траектории точка Р описывает некоторую кривую, называемую годографом скорости точки М. Очевидно, скорость точки годографа Р равна по определению ускорению точки М.
Скорость и ускорение точки в естественной системе координат
Определим орт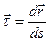 , он касателен к траектории. Составим отношение
, он касателен к траектории. Составим отношение 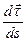 . Вектор dt ортогонален к орту t, так как
. Вектор dt ортогонален к орту t, так как 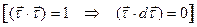
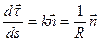 ;где k-кривизна траектории, R-радиус кривизны траектории.
;где k-кривизна траектории, R-радиус кривизны траектории.
Третий орт 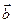 определим как
определим как 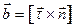
Определим скорость и ускорение точки в естественной системе координат:
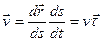 ; т.е.
; т.е. 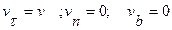
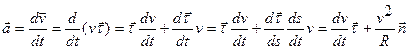
т.е. 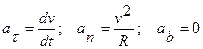
Из последних соотношений получим формулу: 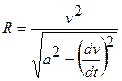
Скорость и ускорение точки в полярных координатах
Положение точки на плоскости известно, если заданы радиус-вектор 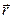 и полярный угол
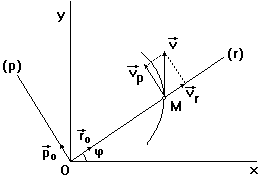
и полярный угол 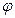 как функции времени:
как функции времени:
| 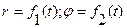 Введем единичный вектор
Введем единичный вектор 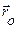 , направленный по радиус-вектору от полюса О к точке М. Тогда , направленный по радиус-вектору от полюса О к точке М. Тогда 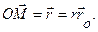 Для скорости получаем: Для скорости получаем:
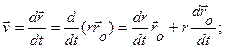
|
Для производной по времени от единичного вектора имеем:
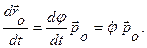
После этого для скорости точки в полярных координатах получаем:
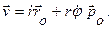
Таким образом радиальная и трансверсальная составляющие вектора скорости имеют вид: 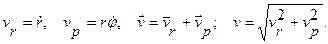
Для ускорения легко получить:
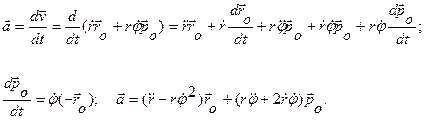
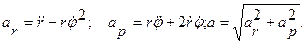
Скорость и ускорение точки в цилиндрических координатах
Положение точки М в пространстве определяют заданием трех ее цилиндрических координат как функций времени:
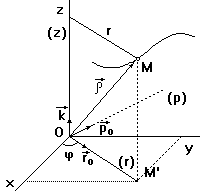
| 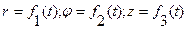 Разложение векторов скорости и ускорения на составляющие, параллельные осям цилиндрической системы координат Or, Op, Oz выразится в следующей форме:
Разложение векторов скорости и ускорения на составляющие, параллельные осям цилиндрической системы координат Or, Op, Oz выразится в следующей форме:
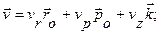
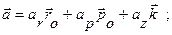
|
где 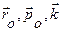 - единичные векторы, направленные по осям цилиндрической системы координат. Оси Or и Op расположены в одной плоскости с осями Ox и Oy.
- единичные векторы, направленные по осям цилиндрической системы координат. Оси Or и Op расположены в одной плоскости с осями Ox и Oy.
Представим радиус-вектор 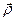 точки М как сумму двух векторов, т.е.
точки М как сумму двух векторов, т.е.
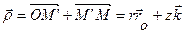
Скорость точки получим дифференцированием радиус-вектора 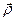 по времени:
по времени:
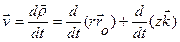
Первое слагаемое в этом выражении вычислялось при выводе скорости точки в полярных координатах. Во втором слагаемом постоянный по модулю и направлению единичный вектор 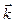 можно вынести за знак производной. В итоге для скорости получается следующее разложение на составляющие осям цилиндрической системы координат:
можно вынести за знак производной. В итоге для скорости получается следующее разложение на составляющие осям цилиндрической системы координат:
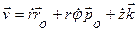
т.е имеем 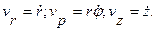 Так как составляющие скорости, параллельные осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля скорости имеем:
Так как составляющие скорости, параллельные осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля скорости имеем:
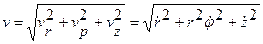
Ускорение точки получим дифференцированием по времени вектора скорости:
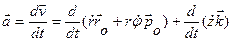
Первое слагаемое в этом выражении вычислялось при выводе ускорения в полярных координатах. Во втором слагаемом орт оси z выносим за знак производной. Получим выражение для ускорения точки в составляющих, параллельных осям цилиндрической системы координат:
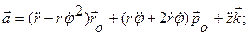
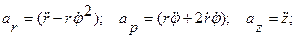

Лекция 6 (кинематика)
«Сложное движение точки»
Движение: абсолютное, относительное, переносное. Теорема Эйлера.
Угловая скорость.
Дополнительно к неподвижным осям Oxyz (система S) введем в рассмотрение некоторое подвижное твердое тело и неизменно связанную с ним систему прямоугольных осей координат O’x’y’z’ (система S’).
Движение точки относительно подвижной системы осей S’ называется относительным движением.
Движение точки относительно неподвижных осей S называется абсолютным движением.
Переносным движением точки за интервал времени (t,t+Dt) называется то движение по отношению к осям S, которая эта точка имела бы, если бы в момент времени t и на интервал (t,t+Dt) она была неизменно связана с подвижной системой осей и, следовательно, перемещалась бы вместе с этой системой.
Траектория, скорость и ускорение называются абсолютными, относительными или переносными, смотря по тому, относятся ли они к движению абсолютному, относительному или переносному.
Теорема Эйлера: Если относительно системы S система S' имеет одну неподвижную точку, то перемещение S' из одного произвольного положения в любое другое может быть совершено одним поворотом на определенный угол относительно оси, проходящей через эту неподвижную точку.
Для доказательства достаточно показать возможность перевода одним поворотом дуги, например, 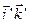 , из положения 1 в положение 2..
, из положения 1 в положение 2..
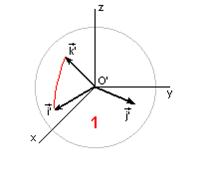
| è | 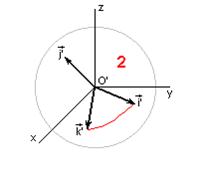
| |
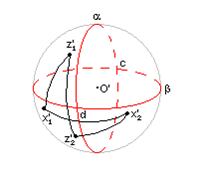
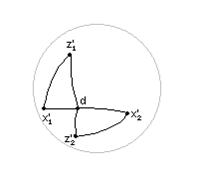
| Обозначим точки  в положении 1 через x1'z1', а в положении 2 через x2' z2'.
Проведем два экватора: a, перпендикулярный середине x1'x2', и b, перпендикулярный середине z1'z2'. Получим две точки пересечения этих экваторов – с и d.
Dx1'z1'd = Dz2'x2'd
(так как x1'z1' = x2'z2', а x1'd = x2'd в силу того, что точка d лежит на экваторе, перпендикулярном середине x1'x2',
z1'd = z2'd по той же причине)
Таким образом, Ðx1'dz1' = Ðz2'dx2' и угол между дугами x1'd и x2'd равен углу между дугами z1'd и z2'd, то есть нужно повернуть x1'z1' относительно оси dO'c на угол x1'dz1' (или равный ему z2'dx2') в положении 1 через x1'z1', а в положении 2 через x2' z2'.
Проведем два экватора: a, перпендикулярный середине x1'x2', и b, перпендикулярный середине z1'z2'. Получим две точки пересечения этих экваторов – с и d.
Dx1'z1'd = Dz2'x2'd
(так как x1'z1' = x2'z2', а x1'd = x2'd в силу того, что точка d лежит на экваторе, перпендикулярном середине x1'x2',
z1'd = z2'd по той же причине)
Таким образом, Ðx1'dz1' = Ðz2'dx2' и угол между дугами x1'd и x2'd равен углу между дугами z1'd и z2'd, то есть нужно повернуть x1'z1' относительно оси dO'c на угол x1'dz1' (или равный ему z2'dx2')
| ||
| |||
Теорема Эйлера справедлива и для конечных и для бесконечно малых поворотов.
При рассмотрении задач о движении тела с одной закрепленной точкой, которые имеют большое практическое значение, для определения (фиксации) положения системы S' относительно S широко используются три угла Эйлера.
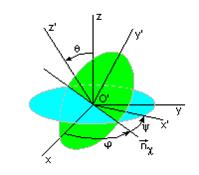
Пересечение плоскостей O'xy и O'x'y' дает прямую, которую называют линией узлов (орт линии узлов -  ). Первый угол Эйлера j - угол между осью O'x и линией узлов. Второй угол y - угол между линией узлов и осью O'x'. Третий угол q - угол между осями O'z и O'z'.
). Первый угол Эйлера j - угол между осью O'x и линией узлов. Второй угол y - угол между линией узлов и осью O'x'. Третий угол q - угол между осями O'z и O'z'.
Эти три угла однозначно определяют положение системы S' относительно S
Таким образом, при бесконечно малом повороте системы S' относительно S на углы dj,dy,dq (некоторые из них могут быть равными нулю) их можно заменить одним поворотом на угол dc вокруг некоторой оси, проходящей через точку O'.
Введем в рассмотрение вектор бесконечно малого поворота:
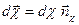 (здесь
(здесь 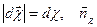 направлен по оси вращения по правилу правого винта)
направлен по оси вращения по правилу правого винта)
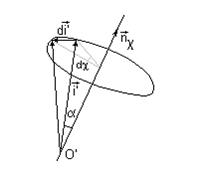
Величина и направление вектора dc при сложном движении могут изменяться. Ось 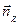 называется осью мгновенного вращения. Посмотрим, что происходит с ортами системы S' при ее повороте на угол
называется осью мгновенного вращения. Посмотрим, что происходит с ортами системы S' при ее повороте на угол 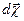
| 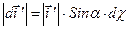
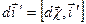 Угловую скорость вращения
Угловую скорость вращения 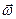 определим следующим образом определим следующим образом
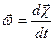 , угловое ускорение , угловое ускорение 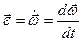 Тогда
Тогда 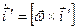 , а также , а также 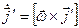 , , 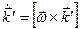 (*) (*)
|
Сложное движение точки.
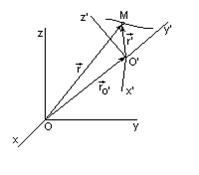
| Рассмотрим движение точки по траектории в пространстве (точка находится в положении М). Будем рассматривать параметры ее движения из неподвижной системы Oxyz и подвижной системы O'x'y'z' (начало отсчета О' может двигаться поступательно и система O'x'y'z' может совершать вращение относительно оси, проходящей через точку О' с угловой скоростью 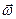 и угловым ускорением и угловым ускорением 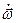 ). Радиус-векторы точки в системах отсчета Oxyz, O'x'y'z', а также радиус-вектор начала отсчета О' в системе Oxyz связаны соотношением: ). Радиус-векторы точки в системах отсчета Oxyz, O'x'y'z', а также радиус-вектор начала отсчета О' в системе Oxyz связаны соотношением:
|
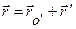
продифференцировав это соотношение по времени, получим:
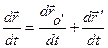
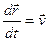 - абсолютная скорость точки (относительно системы S),
- абсолютная скорость точки (относительно системы S),
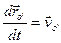 - скорость начала координат S' относительно S,
- скорость начала координат S' относительно S,
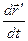 не является скоростью точки М относительно системы S', так как орты этой системы являются функциями времени.
не является скоростью точки М относительно системы S', так как орты этой системы являются функциями времени.
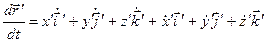 ,
,
используя формулы (*) будем иметь:
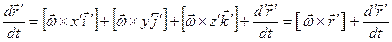
Последнее слагаемое означает, что производная берется при неизменных ортах системы O’x’y’z’, 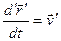 .
.
Теперь для скоростей имеем:
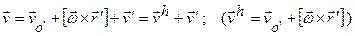
здесь vh-переносная, v – абсолютная, v’ – относительная скорость точки, то есть получена связь этих скоростей. Переносная скорость состоит из двух слагаемых: первое присутствует в том случае, если подвижная система отсчета движется поступательно, второе появляется в том случае, если подвижная система отсчета совершает вращение.
Для получения связи ускорений продифференцируем по времени соотношение для скоростей:
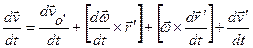
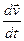 - абсолютное ускорение,
- абсолютное ускорение, 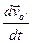 - ускорение начала координат S’ относительно S.
- ускорение начала координат S’ относительно S.
Используем соотношение 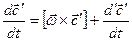 , ранее полученное для
, ранее полученное для 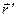 и справедливое для любого вектора, разлагаемого по ортам S’, которая вращается относительно неподвижной системы отсчета.
и справедливое для любого вектора, разлагаемого по ортам S’, которая вращается относительно неподвижной системы отсчета.
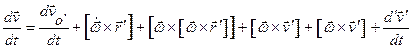
или
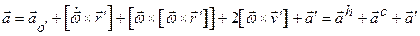
здесь переносное ускорение состоит из трех компонент (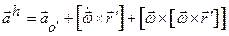 ), первая имеет место, если подвижная система отсчета движется поступательно и при этом неравномерно, вторая появляется при неравномерном вращении подвижной системы отсчета и третья, называемая центростремительным ускорением, присутствует всегда, если подвижная система отсчета просто вращается.
), первая имеет место, если подвижная система отсчета движется поступательно и при этом неравномерно, вторая появляется при неравномерном вращении подвижной системы отсчета и третья, называемая центростремительным ускорением, присутствует всегда, если подвижная система отсчета просто вращается.
Кориолисово ускорение (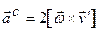 ) присутствует у точки при двух условиях: если подвижная система отсчета вращается и точка движется относительно подвижной системы отсчета и вектор
) присутствует у точки при двух условиях: если подвижная система отсчета вращается и точка движется относительно подвижной системы отсчета и вектор 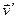 не параллелен вектору
не параллелен вектору 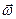 .
.
Кориолисово ускорение на Земле действует на тело, движущееся по поверхности всегда за исключением экваториальной области при движении С «Ю (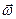 параллельно
параллельно 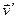 ) или если v’=0 или w=0, первое имеем для всех неподвижных тел. Даже на неподвижное тело действует ускорение
) или если v’=0 или w=0, первое имеем для всех неподвижных тел. Даже на неподвижное тело действует ускорение 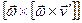 , равное по модулю w2r, где r - расстояние от точки до оси вращения, т.е. вес тела зависит от широты (w2r=(7 x 10-5)2 x 6.3 x 106=0.03 м/с2»0.3% от g).
, равное по модулю w2r, где r - расстояние от точки до оси вращения, т.е. вес тела зависит от широты (w2r=(7 x 10-5)2 x 6.3 x 106=0.03 м/с2»0.3% от g).
Пример. Точка массой m = 75 кг движется по меридиану с юга на север на широте a = 45o с постоянной скоростью v’ = 1 м/с. Угловая скорость вращения Земли 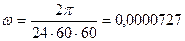 рад/с.
рад/с.
Кориолисово ускорение, действующее на точку равно
ac=-2w v’Sin a=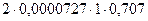 =10-4 м/с2
=10-4 м/с2
Лекция 7 (кинематика)
«Простейшие движения твердого тела, плоское движение»
Степени свободы. Теорема о проекциях
Числом степеней свободы твердого тела называют число независимых параметров, определяющих положение тела относительно рассматриваемой системы координат.
Свободная точка имеет три степени свободы, свободное твердое тело в общем случае имеет шесть степеней свободы. Твердое тело (его положение) может быть задано тремя точками, не лежащими на одной прямой. Расстояния между точками в твердом теле должны оставаться неизменными при любых его движениях. Это накладывает на координаты фиксированных точек три условия. Получаем (3n-k=s)=(9-3=6) шесть степеней свободы.
Теорема. При любом движении твердого тела проекции скоростей двух его точек на прямую, соединяющую эти точки, равны.
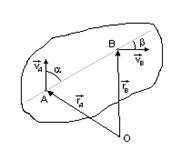
| 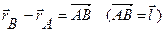 Возведем обе части в скалярный квадрат:
Возведем обе части в скалярный квадрат:
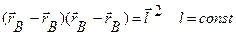 Продифференцируем по времени:
Продифференцируем по времени:
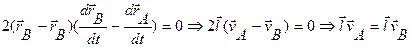
|
Раскладывая скалярные произведения векторов и сокращая на l, имеем: vACosa=vBCosb
Поступательное движение твердого тела
Поступательным движением твердого тела называется такое его движение, при котором любая прямая, жестко связанная с телом, остается параллельной самой себе в каждый момент времени.
Очевидно, достаточно, чтобы это выполнялось только для двух непараллельных прямых, связанных с телом.
Траектории точек у поступательно движущегося твердого тела могут быть не только прямыми, но и любыми кривыми, в том числе окружностями.
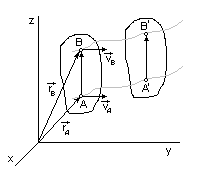
| Теорема. При поступательном движении твердого тела траектории, скорости и ускорения всех точек тела одинаковы.
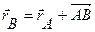 Вектор АВ является всегда постоянным по модулю, а при поступательном движении не изменяется и по направлению.
При сдвиге на АВ траектории точек совпадут.
Вектор АВ является всегда постоянным по модулю, а при поступательном движении не изменяется и по направлению.
При сдвиге на АВ траектории точек совпадут.
|
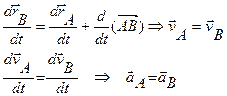
Движение твердого тела, для которого векторы скоростей точек равны только в один момент времени, а не все время, называется мгновенным поступательным движением.
Для мгновенного поступательного движения ускорения точек в общем случае не являются одинаковыми.
Твердое тело, движущееся поступательно, имеет три степенм свободы, так как для описания его движения достаточно задать функции x=f1(t), y=f2(t), z=f3(t) для любой точки и использовать кинематику одной точки.
Вращение твердого тела вокруг неподвижной оси
Вращением твердого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела (или его продолжения) остаются неподвижными в течение всего времени движения.
Прямая, соединяющая эти точки, называется осью вращения.
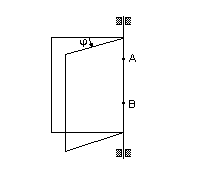
| Положение тела относительно выбранной системы отсчета полностью и однозначно определяется в любой момент времени, если задано уравнение 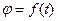 , то есть у тела одна степень свободы.
Угловая скорость , то есть у тела одна степень свободы.
Угловая скорость 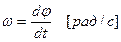 ,
Угловое ускорение ,
Угловое ускорение 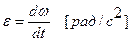
|
Вращение называется равномерным, если w=const
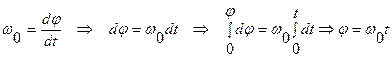
Вращение называется равнопеременным, если e=const
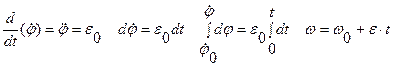
и после второго интегрирования 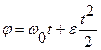
Скорости и ускорения точек тела при вращении
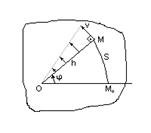
| j = f(t), s = hj
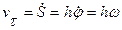 Скорости точек тела при вращении вокруг неподвижной оси пропорциональны их расстояниям до этой оси и перпендикулярны радиусам вращения.
Скорости точек тела при вращении вокруг неподвижной оси пропорциональны их расстояниям до этой оси и перпендикулярны радиусам вращения.
|
Ускорение точки разлагаем на касательную и нормальные составляющие
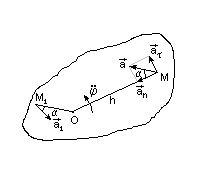
| 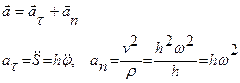 т.к. для окружности r=h
Окончательно
т.к. для окружности r=h
Окончательно 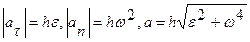
|
Касательные, нормальные и полные ускорения точек, как и скорости, распределены тоже по линейному закону.
Обозначив a угол между полным ускорением точки и ее радиусом вращения, имеем:
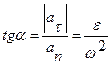
так как нормальное ускорение an всегда положительно.
Угол a для всех точек тела один и тот же. Откладывать его следует от ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения независимо от направления вращения твердого тела.
Пример
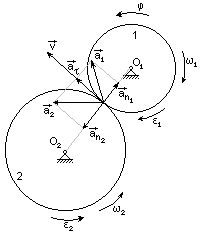
| Диск 1 вращается вокруг неподвижной оси О1 по закону j=(t-t2) и приводит во вращение диск 2. Определить угловые скорости дисков, а также скорости и ускорения точек их соприкосновения А в момент времени t=5c, если r1 =0.2 м, r2 = 0.3 м.
Имеем 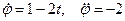 При t=5c
При t=5c 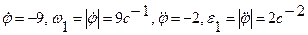 Скорости и касательные ускорения точек соприкосновения дисков 1 и 2 при отсутствии скольжения между ними одинаковы
Скорости и касательные ускорения точек соприкосновения дисков 1 и 2 при отсутствии скольжения между ними одинаковы
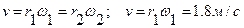
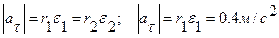
|
Кроме того, 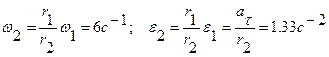
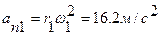
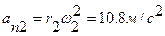
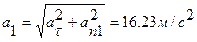
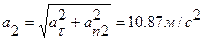
Векторы угловой скорости и ускорения
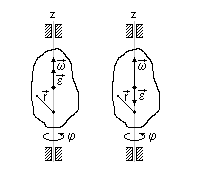
| 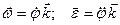
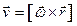 - векторная формула Эйлера - векторная формула Эйлера
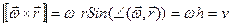 Из параграфа о сложном движении точки считая
Из параграфа о сложном движении точки считая 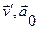 и и 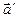 равными нулю имеем равными нулю имеем
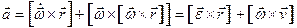 и можем получить все предыдущие результаты для вращения тела вокруг неподвижной оси.
и можем получить все предыдущие результаты для вращения тела вокруг неподвижной оси.
|
Плоское движение твердого тела
Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же неподвижной плоскости. Часто это движение называют плоскопараллельным, так как плоскости, в которых движутся отдельные точки, параллельны между собой.
Траектории точек тела при плоском движении являются плоскими кривыми.
Такой случай движения часто реализуется в технике при движении механизмов и машин.
Вращательное движение твердого тела вокруг неподвижной оси является частным случаем плоского движения.
Для изучения плоского движения твердого тела достаточно рассмотреть движение плоской фигуры в ее плоскости, параллельной неподвижной плоскости P0.
Для задания положения плоской фигуры на плоскости относительно координат Oxy достаточно задать на этой плоскости положение отрезка О'M, скрепленного с фигурой.
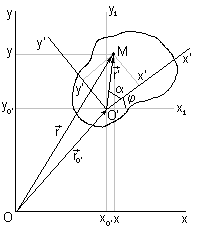
| Скрепим с твердым телом подвижную систему осей O’x’y’
Тогда для координат (x,y) точки М будем иметь:
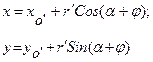 где
где 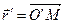 , a - постоянный угол между O’M и осью O’x’
Уравнения движения твердого тела в плоском движении будут иметь вид: xo’ =f1(t); yo’ =f2(t); j = f3(t), то есть, имеем три степени свободы , a - постоянный угол между O’M и осью O’x’
Уравнения движения твердого тела в плоском движении будут иметь вид: xo’ =f1(t); yo’ =f2(t); j = f3(t), то есть, имеем три степени свободы
|
Раскрывая Cos и Sin суммы и учитывая, что r’Cosa=x’, r’Sina=y ’ получаем:
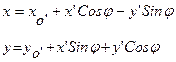
или в векторно-матричной форме
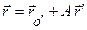 , где
, где
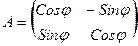 - матрица поворота на плоскости.
- матрица поворота на плоскости.
Эти формулы позволяют определить координаты любой точки плоской фигуры по заданным уравнениям движения этой фигуры и координаты ее точки относительно подвижной системы координат, скрепленной с фигурой.
Лекция 8 (кинематика)
«Скорости и ускорения точек при плоском движении»
Разложение плоского движения твердого тела на поступательное и вращательное
Любое движение твердого тела, в том числе движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых поступательное (переносное), а другое – вращательное (относительное).
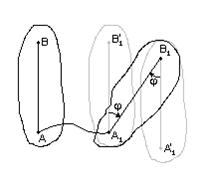
| Пусть тело в своем движении переходит из одного состояния в другое. Мы можем представить это движение двумя способами: 1) тело совершает поступательное перемещение, когда точка А совмещается с А1, потом доворачиваем тело вокруг точки А1, 2) тело совершает поступательное перемещение, когда точка В совмещается с В1, потом доворачиваем тело вокруг точки В1, Точки А1 и В1, вокруг которых мы доворачиваем фигуру, называют полюсами. Нетрудно заметить, что поворот фигуры всегда будет одним и тем же (на угол j), независимо от выбора полюса. Поступательное перемещение зависит от выбора точки – полюса. |
Скорость точек тела при плоском движении. Мгновенный центр скоростей.
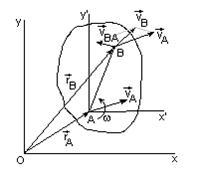
| Выбираем точку А за полюс. Оси подвижной системы координат проведам параллельно неподвижным осям Аx' || Ox; Ay' || Oy. Таким образом, подвижная система координат, движется только поступательно, относительное движение тела будет «чистым» вращением.
Из уравнений для сложного движения точки 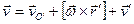 имеем: имеем:
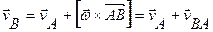
|
Скорость какой-либо точки фигуры при ее плоском движении равна векторной сумме скорости полюса (переносной) и относительной скорости этой точки от вращения фигуры вокруг полюса. Эта формула выражает зависимость между скоростями двух любых точек тела при плоском движении в любой момент времени.
В каждый момент времени при плоском движении фигуры, если w¹0, имеется единственная точка этой фигуры (или ее продолжения), скорость которой равна нулю. Эту точку называют мгновенным центром скоростей. Обозначим ее Р.
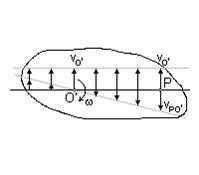
| Необходимо указать способ нахождения полюса. Пусть есть плоская фигура, нам известна скорость движения ее полюса О' и угловая скорость вращения вокруг полюса - w.
Скорость точки Р равна нулю, если 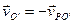 . Мгновенный центр скоростей находится на перпендикуляре к скорости . Мгновенный центр скоростей находится на перпендикуляре к скорости 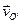 , проведенном из точки О', на расстоянии , проведенном из точки О', на расстоянии 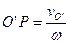 . .
|
Мгновенный центр скоростей является единственной точкой плоской фигуры для данного момента времени. В другой момент времени в общем случае мгновенным центром является уже другая точка плоской фигуры.
Если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют также, как и в случае вращения фигуры в рассматриваемый момент времени вокруг своего мгновенного центра скоростей с угловой скоростью w.
Способы нахождения мгновенного центра скоростей.
Мгновенный центр скоростей можно найти либо из механических условий задачи (точка касания колеса, катящегося без проскальзывания), либо по скоростям точек плоской фигуры.
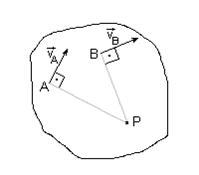
| Если известны скорости двух точек плоской фигуры, мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек | ||
| В том случае, когда точки лежат на общем перпендикуляре к скоростям этих точек и скорости точек параллельны, концы векторов скоростей точек лежат на одной прямой, проведенной через мгновенный центр скоростей, так как скорости точек пропорциональны расстояниям от этих точек до центра скоростей. | 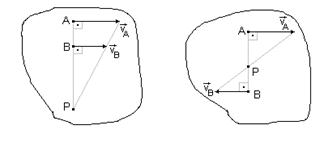
| ||
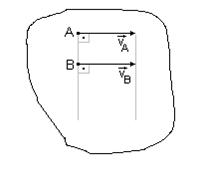
| Если скорости двух точек, расположенных на общем перпендикуляре к этим скоростям, еще и равны, мгновенный центр скоростей находится на бесконечности и мы имеем мгновенное поступательное движение плоской фигуры, при котором скорости всех точек фигуры одинаковы по модулю и направлению, w=0. При этом мгновенном поступательном движении только скорости точек одинаковы, а их ускорения в общем случае различны. | ||
| Невозможен случай, когда скорости двух точек, не лежащих на общем перпендикуляре к скоростям, не равны друг другу по модулю, но параллельны, так как для него не выполняется теорема о проекциях скоростей на прямую, соединяющую эти точки. | 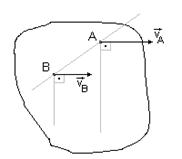
| ||
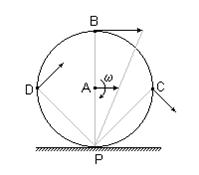
| Пример. У колеса, катящегося по горизонтальной плоскости без проскальзывания со скоростью v0, мгновенным центром скоростей является точка контакта колеса с плоскостью.
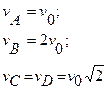
|
Вычисление угловой скорости при плоском движении.
Угловую скорость плоской фигуры при плоском движении можно вычислить, согласно определению, как
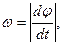
Также ее можно определить так:
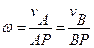
Величину w можно вычислить путем предварительного нахождения скорости какой-либо точки плоской фигуры от вращения фигуры вокруг другой ее точки, принятой за полюс: 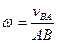 , знак угловой скорости определяют по направлению относительной скорости.
, знак угловой скорости определяют по направлению относительной скорости.
Еще один способ такой: если предварительно установить зависимость угла поворота плоской фигуры от линейных угловых величин других плоских фигур тождественным соотношением, то дифференцируя его по времени, получаем соотношение, из которого иногда удается определить искомую угловую скорость.
|
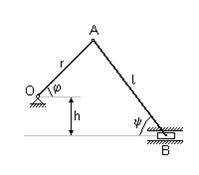
Пример. В несимметричном (смещенном) кривошипно-шатунном механизме установить зависимость между угловыми скоростями кривошипа OA - w и шатуна AB - w1:
Для j<p/ 2 r Sinj + h = l Siny
После дифференцирования 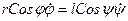 Учитывая, что
Учитывая, что 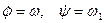 , получаем: , получаем: 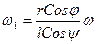 (при h=0 и r= l w = w1)
(при h=0 и r= l w = w1)
|
Ускорения точек при плоском движении. Мгновенный центр ускорений.
За переносное движение тела примем поступательное движение, за относительное движение – вращение тела вокруг полюса А.
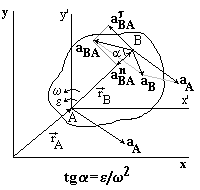 Полюс А движется с ускорением aA и тело вращается вокруг полюса с угловой скоростью w и угловым ускорением e. Из формул для сложного движения точки имеем:
Полюс А движется с ускорением aA и тело вращается вокруг полюса с угловой скоростью w и угловым ускорением e. Из формул для сложного движения точки имеем:
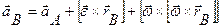
Эту формулу можно представить в виде:
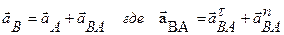
Ускорение aBA точка В получает из-за вращения вокруг полюса А, компоненты этого ускорения определяются так:
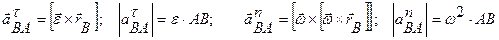
отсюда 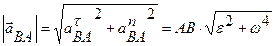
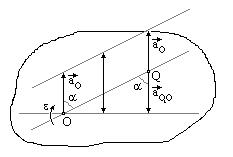 Мгновенный центр ускорений. В каждый момент движения плоской фигуры в своей плоскости, если w и e не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений, мы будем ее обозначать Q.
Мгновенный центр ускорений. В каждый момент движения плоской фигуры в своей плоскости, если w и e не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений, мы будем ее обозначать Q.
Пусть нам известны по модулю и направлению ускорение какой-либо точки плоской фигуры (точка О), угловая скорость и угловое ускорение e этой фигуры.
Мгновенный центр ускорений лежит на прямой, проведенной под углом a (tga=e/w2) к ускорению точки О. При этом a надо отложить от ускорения aO в направлении дуговой стрелки углового ускорения e.
Только в точках этой прямой ускорение aO и ускорение от вращения aQO могут иметь противоположные направления и одинаковые по модулю значения.
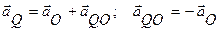
Но 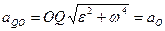 , следовательно
, следовательно 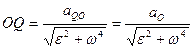 .
.
Мгновенный центр ускорений является единственной точкой фигуры, ускорение которой в рассматриваемый момент времени равно нулю. В другой момент времени мгновенный центр ускорений находится в общем случае в другой точке плоской фигуры.
Если положение мгновенного центра ускорений известно, то выбрав его за полюс, для ускорения произвольной точки А имеем:
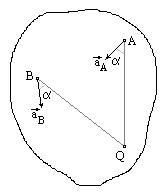
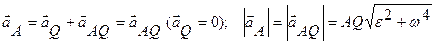
и ускорение aA направлено под углом a к отрезку AQ, соединяющего точки A и Q в сторону дуговой стрелки e.
Ускорения двух точек A и B показаны на рисунке, их величины равны
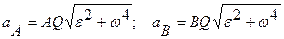
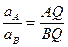
Итог: ускорения точек плоской фигуры при плоском движении можно определить также, как и при вращательном движении плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью w и угловым ускорением e.
Для вычисления скоростей принимают, что фигура вращается вокруг мгновенного центра скоростей, для вычисления ускорений принимают, что фигура вращается вокруг мгновенного центра ускорений. В общем случае эти центры являются разными точками плоской фигуры.
Ускорения точек плоской фигуры при плоском движении подобно скоростям точек можно вычислить двумя способами: по формуле 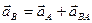 , выражающей зависимость ускорений двух точек плоской фигуры (способ 1) и по формуле
, выражающей зависимость ускорений двух точек плоской фигуры (способ 1) и по формуле 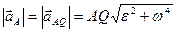 , используя мгновенный центр ускорений (способ 2). Часто мгновенный центр ускорений (кроме случаев w или e равных нулю) располагается так, что трудно определить расстояние от него до рассматриваемых точек фигуры, поэтому рекомендуется использовать способ 1 через формулу, связывающую ускорения точек фигуры.
, используя мгновенный центр ускорений (способ 2). Часто мгновенный центр ускорений (кроме случаев w или e равных нулю) располагается так, что трудно определить расстояние от него до рассматриваемых точек фигуры, поэтому рекомендуется использовать способ 1 через формулу, связывающую ускорения точек фигуры.
Способы нахождения мгновенного центра ускорений.
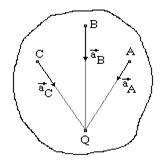 1.
1. 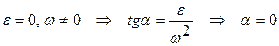
Ускорения всех точек направлены к мгновенному центру ускорений, так как они состоят только из одной нормальной составляющей от вращения вокруг мгновенного центра ускорений. Если известно aA, то AQ=aA/w2.
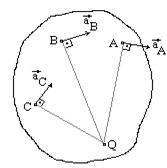 2.
2. 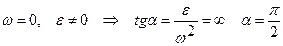
(мгновенное поступательное движение)
Мгновенный центр ускорений лежит на пересечении перпендикуляров к ускорениям точек. Если известно aA, то AQ=aA/e
3. 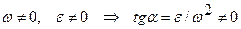
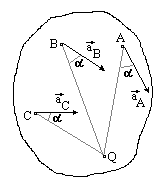 Имеем общий случай, ранее уже обсуждавшийся. Угол a откладываем по дуговой стрелке e от вектора ускорения.
Имеем общий случай, ранее уже обсуждавшийся. Угол a откладываем по дуговой стрелке e от вектора ускорения.
Если известно aA, то 
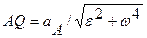
1. Пусть в данный момент времени известны ускорения двух точек плоской фигуры A и B. Приняв за полюс точку A, имеем:
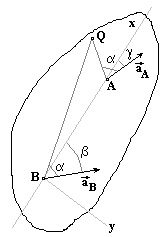
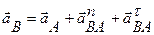 (*)
(*)
где 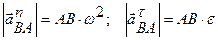
Проецируя левую и правую части векторной формулы (*) на оси Bx и BY получаем:
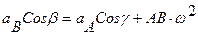
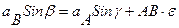
Здесь b и g в принципе известные углы.
Проекцию anBA на ось Вх берем со знаком (+), так как она всегда направлена к оси вращения. Проекцию atBA, берем со знаком (+) предполагая, что стрелка e направлена против часовой стрелки.
Из уравнений проекций находим
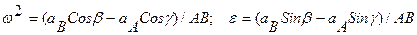
знак e определяется после подстановки данных в формулу.
После того, как найдены e и w, задача нахождения мгновенного центра ускорений сводится к случаю 3.
Вычисление углового ускорения при плоском движении.
1. Если известен угол поворота фигуры как функция времени, то
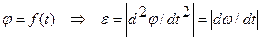
2. Находим мгновенный центр скоростей и, зная скорость некоторой точки А, находим угловую скорость w вращения фигуры
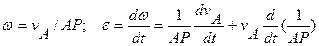
если AP – const, то 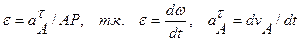
Пример.
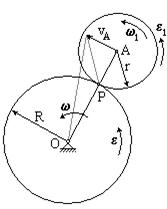 Кривошип OA вращается с угловой скоростью w и угловым ускорением e вокруг центра О. Колесо радиуса r катится без скольжения по колесу радиуса R. Найдем угловую скорость и угловое ускорение вращения колеса радиуса r.
Кривошип OA вращается с угловой скоростью w и угловым ускорением e вокруг центра О. Колесо радиуса r катится без скольжения по колесу радиуса R. Найдем угловую скорость и угловое ускорение вращения колеса радиуса r.
Мгновенным центром скоростей подвижного колеса является точка P. Тогда w1 = vA/AP = vA/r. Но в то же время точка А совершает вращение вокруг точки О с угловой скоростью w.
w = vA/AO = vA/(r + R)
Отсюда получаем 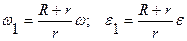
При внутреннем зацеплении колес дуговые стрелки w и e колеса и кривошипа имеют потивоположные направления.
3. Иногда угловое ускорение e плоской фигуры можно найти путем проецирования на оси координат известного по направлению ускорения (например, точки В), если ускорение какой-либо другой точки А и угловая скорость фигуры w известны или их можно вычислить предварительно.
При этом используем формулу 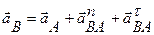 и проецирование ведем на ось, перпендикулярную aB .
и проецирование ведем на ось, перпендикулярную aB .
Пример.
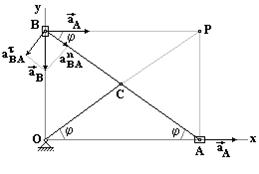 Кривошип OC приводит в движение линейку эллипсографа AB, один конец которой с помощью ползуна В удерживается на оси y, другой конец A – на оси x. Ускорение точки В направлено вдоль оси y. Рассмотрим проекцию вышеприведенной формулы на ось x:
Кривошип OC приводит в движение линейку эллипсографа AB, один конец которой с помощью ползуна В удерживается на оси y, другой конец A – на оси x. Ускорение точки В направлено вдоль оси y. Рассмотрим проекцию вышеприведенной формулы на ось x:
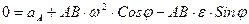
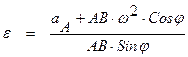
Этот метод подходит для шатунов, у которых есть точка, которая движется прямолинейно.
Если же известны ускорения двух точек А и В по модулю и направлению, то мы имеем случай 4 для нахождения мгновенного центра ускорений (проецируем формулу для связи ускорений на направление АВ и перпендикулярное ему).
4. 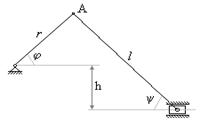 В задачах, где можно определить тождественное соотношение между углами поворота, проводим двойное дифференцирование. В ранее рассмотренном примере для мгновенного центра скоростей мы получили
В задачах, где можно определить тождественное соотношение между углами поворота, проводим двойное дифференцирование. В ранее рассмотренном примере для мгновенного центра скоростей мы получили 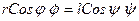 .
.
Дифференцируя вторично, будем иметь
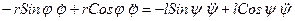
Если dj/dt=w-const, то 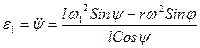
Лекция 9 (динамика)
«Классификация сил, динамика материальной точки. Основные виды прямолинейного движения точки. Криволинейное движение»
Часть III Динамика
Классификация сил. Динамика материальной точки.
Силу оценивают по движению, которое она вызывает или стремится вызвать в рассматриваемой системе координат, которую мы условились считать неподвижной (инерциальной).
а) Потенциальные силы – силы, которые могут быть выражены через некоторую скалярную функцию от положения точки, называемой потенциальной энергией.
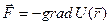
Работа на конечном перещении точки из положения 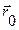 в положение
в положение 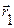 равна определенному интегралу
равна определенному интегралу
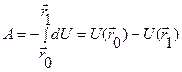 ,
,
т.е. не зависит от формы траектории, является только функцией начального и конечного положения.
б) Гироскопические силы 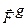 - линейно зависят от скорости точки и всегда направлены перпендикулярно этой скорости, работа гироскопических сил, очевидно, всегда равна нулю (примеры – сила инерции Кориолиса, магнитная часть силы Лоренца).
- линейно зависят от скорости точки и всегда направлены перпендикулярно этой скорости, работа гироскопических сил, очевидно, всегда равна нулю (примеры – сила инерции Кориолиса, магнитная часть силы Лоренца).
в) Диссипативные силы 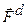 - направлены всегда противоположно скорости тела относительно среды, вызывающей торможение.
- направлены всегда противоположно скорости тела относительно среды, вызывающей торможение.
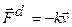 ,
,
где k – положительная скалярная функция, которая может зависеть от положения и скорости тела. Всегда A(Fd) < 0 – работа диссипативных сил (сил сопротивления) всегда отрицательна.
Вся динамика построена на предположении о том, что в природе существуют
 2014-02-13
2014-02-13 592
592








