2014-02-13
479
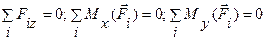
имеем три уравнения
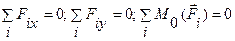(для любой точки)
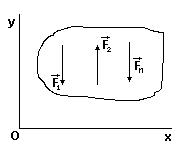
Для плоской системы параллельных сил имеем два уравнения равновесия:
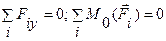(для любой точки)
Теорема о моменте равнодействующей силы (теорема Вариньона)
Пусто система сил не находится в равновесии и может быть приведена к равнодействующей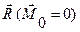 
.
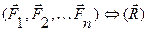
Добавим к этой системе сил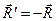 
, тогда
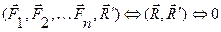
Эта новая система сил, эквивалентная нулю, удовлетворяет условиям равновесия системы сил и, в частности, условию равенства нулю суммы векторных моментов сил относительно любой точки:
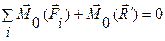
Т.к.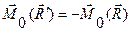 
, то имеем теорему Вариньона
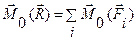
Это справедливо и в любых проекциях, например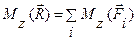 
, т.е. для плоской системы сил имеем теорему Вариньона в алгебраических моментах
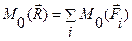
Различные формы условий равновесия плоской системы сил:
1. Ранее приведенная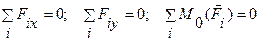 
2. Эквивалентная ей система уравнений равновесия
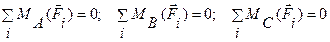
для любых трех точек, не лежащих на одной прямой.
3. Также эквивалентная первой система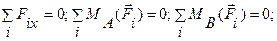 
для любых точек А и В, если ось х не перпендикулярна отрезку АВ.
Для равновесия плоской системы параллельных сил имеем альтернативную форму условий равновесия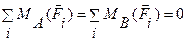 
для любых точек А и В:
|
|
|
Статически определимые и неопределимые задачи
Для любой системы сил для разрешимости задач необходимо, чтобы число неизвестных сил не превышало максимального числа возможных уравнений равновесия. Такие задачи называют статически определимыми. В противном случае задача статически неопределима в рамках моделей твердых тел.
Равновесие системы тел
При рассмотрении равновесия системы сил, приложенных к системе нескольких взаимодействующих между собой тел, мысленно расчленяем систему на части и внутренние силы для части считаем внешними силами. Внутренние силы образуют по аксиоме о взаимодействии равновесную систему (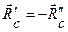
).
Распределенные силы
