Задача 2. Решить задачу о лакокрасочной фабрике симплекс-методом.
Математическая модель задачи (смотрите пример1):
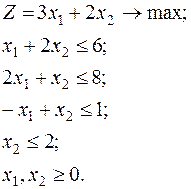 (1)
(1)
Приведём задачу к каноническому виду, приводя ограничения типа ˝ 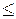 ˝ к ограничениям типа ˝=˝, вводя неотрицательные остаточные переменные S1, S2, S3, S4, причём,
˝ к ограничениям типа ˝=˝, вводя неотрицательные остаточные переменные S1, S2, S3, S4, причём, 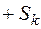 , если знак в ограничении
, если знак в ограничении 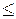 , и
, и 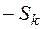 , если знак
, если знак 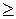 .
.
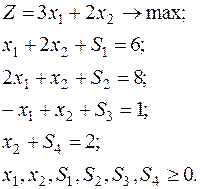 (2)
(2)
Выпишем расширенную матрицу ограничений (коэффициенты при неизвестных в ограничениях):
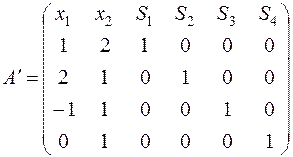 .
.
В матрице 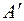 имеется единичная подматрица, число строк в которой равно количеству ограничений. Поэтому задача имеет очевидный начальный базис
имеется единичная подматрица, число строк в которой равно количеству ограничений. Поэтому задача имеет очевидный начальный базис 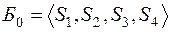 , т.к. столбцы единичной подматрицы соответствуют этим переменным.
, т.к. столбцы единичной подматрицы соответствуют этим переменным.
Замечание 1. Единичная подматрица может получаться и путём перестановки столбцов.
Подставляем эти выражения в целевую функцию для получения Z-строки начальной симплекс-таблицы.
Замечание 2. В данной задаче базисные переменные можно было бы не выражать, т.к. Z не содержит базисных переменных.
Переносим в Z неизвестные в левую часть:
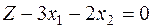 - Z-строка начальной симплекс-таблицы.
- Z-строка начальной симплекс-таблицы.
Строим начальную симплекс-таблицу (смотрите таблицу 1) и доводим её до оптимальной.
Таблица1
| Б | Z | x1 | x2 | S1 | S2 | S3 | S4 | Реш. | 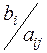
| Ком. |
| Z | -3 | -2 | - | Не опт. | ||||||
| S1 | x1→Б | |||||||||
| S2 | Б→S2 | |||||||||
| S3 | -1 | - | ||||||||
| S4 | - |
Данная симплекс-таблица не оптимальна, т.к. в Z-строке у переменных есть отрицательные коэффициенты (относительные оценки). Выбираем наименьшую отрицательную относительную оценку и эта переменная входит в базис: x1→Б (ведущий столбец). Делим элементы столбца ˝Решение˝ на положительные элементы ведущего столбца x1 и результаты записываем в столбец 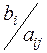 . Выбираем в столбце
. Выбираем в столбце 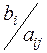 наименьшее число и эта переменная выходит из базиса: Б→S2 (ведущая строка). Обнуляем элементы ведущего столбца методом Гаусса (на пересечении ведущей строки и ведущего столбца получаем 1, а остальные 0). Следующую симплекс-таблицу (таблица 2) получаем следующим образом:
наименьшее число и эта переменная выходит из базиса: Б→S2 (ведущая строка). Обнуляем элементы ведущего столбца методом Гаусса (на пересечении ведущей строки и ведущего столбца получаем 1, а остальные 0). Следующую симплекс-таблицу (таблица 2) получаем следующим образом: 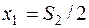 ;
; 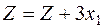 ;
; 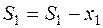 ;
; 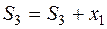 ;
; 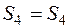 .
.
Таблица 2
| Б | Z | x1 | x2 | S1 | S2 | S3 | S4 | Реш. | 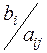
| Ком. |
| Z | -1/2 | 3/2 | - | Не опт. | ||||||
| S1 | 3/2 | -1/2 | 4/3 | x2→Б | ||||||
| x1 | 1/2 | 1/2 | Б→S1 | |||||||
| S3 | 3/2 | 1/2 | - | |||||||
| S4 | - |
Замечание 3. Приобнулении ведущего столбца можно прибавлять или вычитать либо ведущую строку или строку, полученную из ведущей.
Таблица 2 не оптимальна. Для получения следующей таблицы 3 обнуляем элементы столбца x2.
Таблица 3
| Б | Z | x1 | x2 | S1 | S2 | S3 | S4 | Реш. | 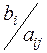
| Ком. |
| Z | 1/3 | 4/3 | 12 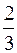
| - | опт. | |||||
| x2 | 2/3 | -1/3 | 4/3 | - | ||||||
| x1 | -1/3 | 2/3 | 10/3 | - | ||||||
| S3 | -1 | - | ||||||||
| S4 | -2/3 | 1/3 | 2/3 | - |
Получена оптимальная симплекс-таблица. Значения базисных переменных и 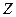 находятся в столбце ˝Решение˝, а значения небазисных переменных равны нулю.
находятся в столбце ˝Решение˝, а значения небазисных переменных равны нулю.
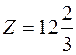 - максимальная прибыль.
- максимальная прибыль.
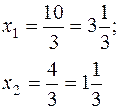 - объёмы производства.
- объёмы производства.
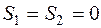 , т.к.
, т.к. 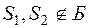 .
.
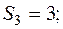
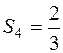 .
.
Проверка (подставляем значения базисных переменных в канонический вид):
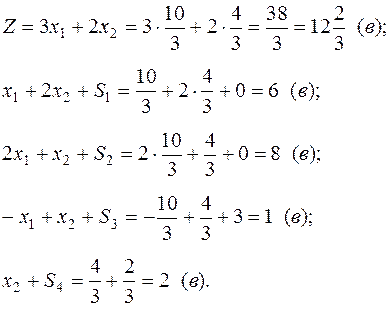
 2015-01-21
2015-01-21 372
372








