Задача 3. Решить задачу линейного программирования, заданную в каноническом виде и имеющую очевидный начальный базис:
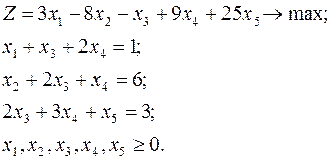
Выпишем матрицу ограничений:
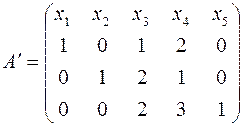 .
.
Очевидный начальный базис 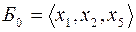 , т.к. путем перестановки столбцов при этих переменных получается единичная подматрица.
, т.к. путем перестановки столбцов при этих переменных получается единичная подматрица.
Выражаем из ограничений базисные переменные 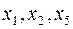 через небазисные:
через небазисные: 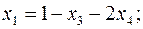
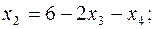
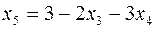 и подставляем в
и подставляем в 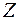 :
:
. 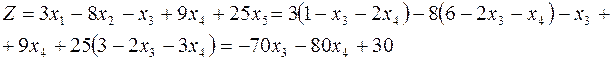
Переносим неизвестные влево:
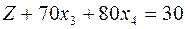 - Z-строка начальной симплекс-таблицы.
- Z-строка начальной симплекс-таблицы.
Строим начальную симплекс-таблицу (смотрите таблицу 4).
Таблица4
| Б | Z | x1 | x2 | x3 | x4 | x5 | Реш. | 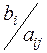
| Ком. |
| Z | - | Опт. | |||||||
| x1 | - | ||||||||
| x2 | - | ||||||||
| x5 | - |
Данная симплекс-таблиц оптимальна,. Получаем
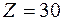 - максимальное значение при значениях переменных:
- максимальное значение при значениях переменных:
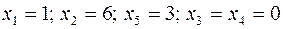 .
.
Проверка:
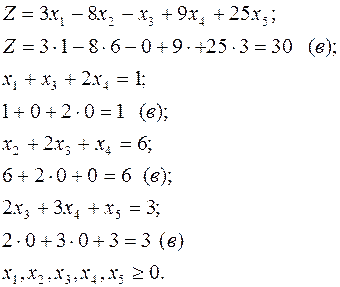
 2015-01-21
2015-01-21 426
426








