2015-01-21
568
Гиперболой называется множество точек, разность расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.
Выбирая систему, координат так же, как и для эллипса, уравнение гиперболы можно записать в каноническом виде:
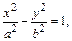
где число а называется действительной полуосью гиперболы, а число b – мнимой полуосью; а, b >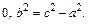 
Прямые y =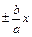 
являются асимптотами гиперболы. Вид кривой показан на рис.3.
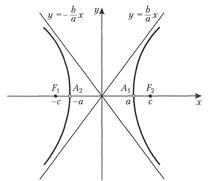
Рис.3
Эксцентриситет гиперболы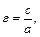 
где а –действительная полуось. Так как у гиперболы с > a, то ее эксцентриситет 
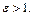Величина эксцентриситета гиперболы определяет форму ее ветвей. При увеличении эксцентриситета увеличивается размах ветвей гиперболы.
