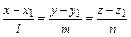 (11)
(11)
определяют прямую, проходящую через точку 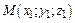 и параллельно вектору
и параллельно вектору 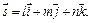
6. Угол между двумя прямыми, заданными их каноническими уравнениями 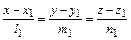 и
и 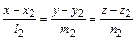 , определяется по формуле
, определяется по формуле
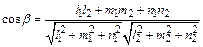 . (12)
. (12)
7. Угол между прямой 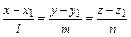 и плоскостью
и плоскостью 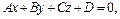 определяется по формуле
определяется по формуле
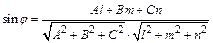 . (13)
. (13)
Пример 3. Даны координаты вершин пирамиды 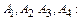
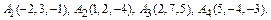 Составить уравнение прямой, проходящей через
Составить уравнение прямой, проходящей через 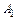 и
и 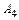 ; составить уравнения плоскостей
; составить уравнения плоскостей 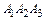 и
и 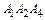 ; найти угол между ребром
; найти угол между ребром 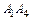 и гранью
и гранью 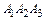 ; найти угол между плоскостями
; найти угол между плоскостями 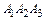 и
и 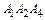 ; найти расстояние от точки
; найти расстояние от точки 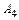 до плоскости
до плоскости 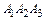 ; составить уравнение плоскости, проходящей через вершину
; составить уравнение плоскости, проходящей через вершину 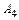 параллельно плоскости
параллельно плоскости 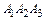 .
.
Решение. 1. Подставив координаты вершин 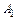 и
и  в формулу (10), получим уравнение прямой
в формулу (10), получим уравнение прямой
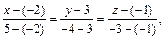
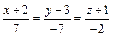 (
(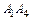 ).
).
2. Уравнение плоскости 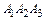 получим, подставив координаты вершин
получим, подставив координаты вершин 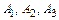 в формулу (6):
в формулу (6):
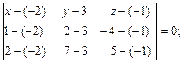
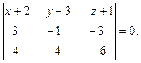
Вычислим определитель разложением по элементам 1-ой строки
(х +2) 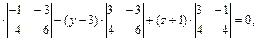
т.е.
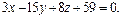
Аналогично получаем уравнение плоскости 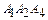 :
: 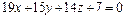 .
.
3. Угол между ребром 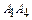 и гранью
и гранью 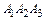 найдем по формуле (13), подставив
найдем по формуле (13), подставив 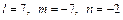 ,
, 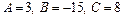 .
.
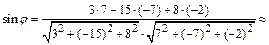 0,63,
0,63,
откуда 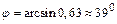 =0,68 рад.
=0,68 рад.
4. По уравнениям плоскостей 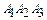 и
и 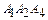 определяем их нормальные векторы:
определяем их нормальные векторы: 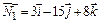 ,
, 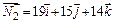 . Угол между плоскостями находим по формуле (7):
. Угол между плоскостями находим по формуле (7):
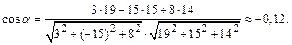
Отсюда следует, что 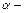 тупой угол, равный
тупой угол, равный 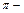
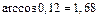 рад с точностью до 0,01. Это и есть искомый угол между плоскостями
рад с точностью до 0,01. Это и есть искомый угол между плоскостями 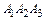 и
и 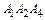 .
.
5. Расстояние от точки 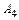 (
(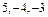 ) до плоскости
) до плоскости 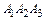 найдем по формуле (8):
найдем по формуле (8):
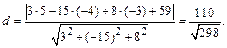
6. Уравнение плоскости, проходящей через вершину 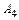 (
(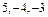 ) параллельно плоскости
) параллельно плоскости 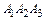 с нормальным вектором
с нормальным вектором 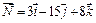 , получим по формуле (9):
, получим по формуле (9):
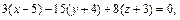
т.е.
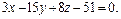
 |
 2015-01-21
2015-01-21 513
513








