Постановка задачи. Найти неопределенный интеграл
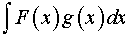 .
.
План решения. Пусть 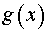 имеет очевидную первообразную
имеет очевидную первообразную 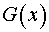 , а
, а 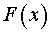 – дифференцируемая функция, причем ее производная
– дифференцируемая функция, причем ее производная 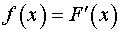 является более простой функцией, чем
является более простой функцией, чем 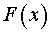 . Тогда применяем формулу интегрирования по частям
. Тогда применяем формулу интегрирования по частям
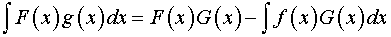 .
.
Если метод избран удачно, то интеграл в правой части этого равенства оказывается табличным или известным образом сводится к табличному, например, повторным интегрированием по частям.
Примечание 1. Чаще всего в учебниках и справочных пособиях встречается следующая формула интегрирования по частям (обозначения которой мы и используем в решениях):
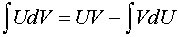 .
.
Примечание 2. В случае определенного интеграла имеем формулу
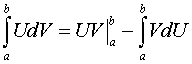 .
.
Задача 2. Вычислить определенные интегралы.
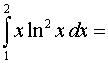
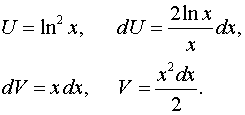
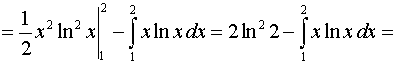
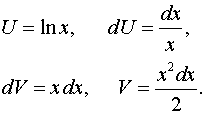
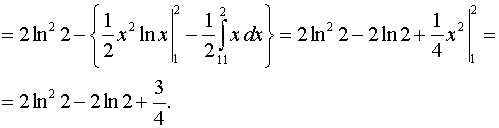
 2015-01-21
2015-01-21 430
430








