Пусть задана дифференцируемая функция 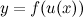 . Тогда
. Тогда
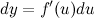
где 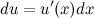 в общем случае не является постоянной величиной. Поэтому дифференциал от функции
в общем случае не является постоянной величиной. Поэтому дифференциал от функции 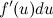 берем как дифференциал от произведения
берем как дифференциал от произведения
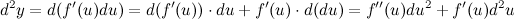
Пример
Задание. Найти дифференциал второго порядка 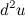 функции
функции 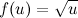 , где
, где 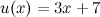 и
и  - независимая переменная.
- независимая переменная.
Решение. Решим пример разными способами и сравним ответы.
1-ый способ. Согласно формуле, имеем, что искомый дифференциал
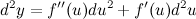
Найдем все необходимые компоненты формулы. Из условия имеем:
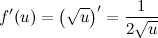
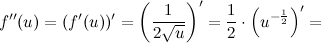
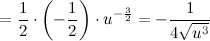
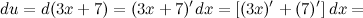
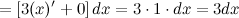
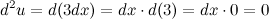
А тогда:
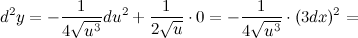
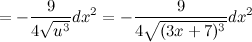
2-ой способ. Из того, что 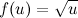 и
и 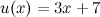 , получаем:
, получаем:
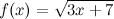
А тогда
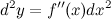
Найдем вторую производную функции 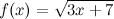 :
:
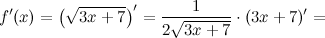
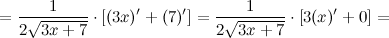
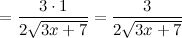
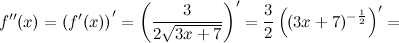
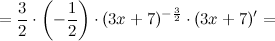
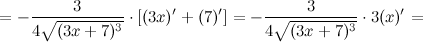
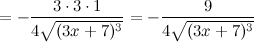
Окончательно имеем:
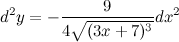
Ответ. 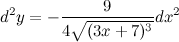
 2015-01-21
2015-01-21 377
377








