Пусть функция U = F (X, Y, Z) непрерывна в некоторой области D и имеет в этой области непрерывные частные производные. Выберем в рассматриваемой области точку M(X,Y,Z) и проведем из нее вектор S, направляющие косинусы которого cos A, cos B, cos G. На векторе S на расстоянии D S от его начала найдем точку М 1(Х+ D Х, у+ D У,Z+ D Z), где
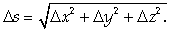
Представим полное приращение функции F в виде:

После деления на Δ S получаем:
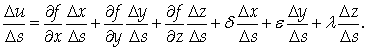
Поскольку
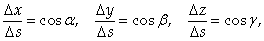
Предыдущее равенство можно переписать в виде:
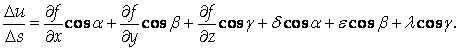
Предел отношения 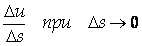 Называется Производной от функции U = F (X, Y, Z) По направлению вектора S и обозначается Называется Производной от функции U = F (X, Y, Z) По направлению вектора S и обозначается 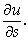 |
При этом
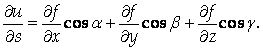 |
Замечание 1. Частные производные являются частным случаем производной по направлению. Например, при
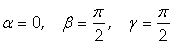
Получаем:
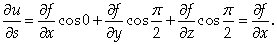
Замечание 2. Выше определялся геометрический смысл частных производных функции двух переменных как угловых коэффициентов касательных к линиям пересечения поверхности, являющейся графиком функции, с плоскостями Х = х0 И У = у0. Аналогичным образом можно рассматривать производную этой функции по направлению L в точке М(х0, у0) как угловой коэффициент линии пересечения данной поверхности и плоскости, проходящей через точку М параллельно оси O Z и прямой L.
| Вектор, координатами которого в каждой точке некоторой области являются частные производные функции U= F (X, Y, Z) в этой точке, называется Градиентомфункции U = F (X, Y, Z). |
Обозначение:
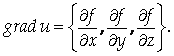
Свойства градиента
1. Производная 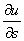 по направлению некоторого вектора S Равняется проекции вектора grad U на вектор S.
по направлению некоторого вектора S Равняется проекции вектора grad U на вектор S.
Доказательство.
Единичный вектор направления S имеет вид ES ={cosα, cosβ, cosγ}, поэтому правая часть формулы (4.7) представляет собой скалярное произведение векторов grad U и Es, то есть указанную проекцию.
2. Производная в данной точке по направлению вектора S имеет наибольшее значение, равное |grad U |, если это направление совпадает с направлением градиента.
Доказательство.
Обозначим угол между векторами S И grad U Через J. Тогда из свойства 1 следует, что
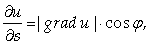
Следовательно, ее наибольшее значение достигается при J =0 и равно |grad U |.
3. Производная по направлению вектора, перпендикулярного к вектору grad U, равна нулю.
Доказательство.
В этом случае
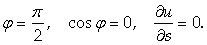
4. Если Z = F (X,Y) – функция двух переменных, то
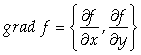
Направлен перпендикулярно к линии уровня F (X,Y) = C, проходящей через данную точку.
 2015-01-21
2015-01-21 1162
1162
