Свойства действий над событиями

1. Объединение и пересечение коммутативны:

AÈB = BÈA; AÇB = BÇA, или

A+B=B+A; AB=BA.

2. Объединение и пересечение ассоциативны:

(AÈB)ÈC=AÈ(BÈC)=(AÈC) ÈB=AÈBÈC.

(AÇB)ÇC=AÇ(BÇC)=(AÇC)ÇB=AÇBÇC;

3. Объединение и пересечение событий дистрибутивны:

(AÈB)C=ACÈBC.

4. Для любых A и B справедливо

.

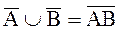Обобщение на n событий:

.

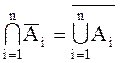5. Для любых A и B справедливо: 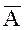Ç =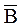

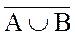
Обобщение на n событий: .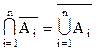

Свойства 4 и 5 выражают принцип двойственности (или правила де-Моргана): операции объединения и пересечения меняются местами при переходе к противоположным событиям.

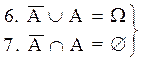действия с противоположными событиями.

8. Объединение (сумма) полной группы событий А₁, А₂,..., А_n представляет собой достоверное событие:

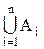=W.

9. Любое событие А можно разложить на сумму несовместных (непересекающихся) событий: A=AW=A(B+ 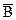)=AB+A .

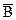Нетрудно видеть, что операции (действия) над событиями тождественны операциям над множествами.

Вероятность и её свойства.

Любому случайному событию в данном опыте можно поставить в соответствие числовую характеристику, определяющую степень возможности появления этого события. Она называется вероятностью. Понятие вероятности является одним из основных понятий при построении вероятностной модели случайного явления. Используя введенное ранее понятие «пространство элементарных событий», дадим современное определение вероятности, базирующееся на аксиоматике Колмогорова.

Пусть задано некоторое пространство элементарных событий W и некоторая система E множеств A,которые являются событиями: AÎW.

С помощью операций объединения: «È», пересечения: «Ç» и разности: «\» можно из элементов E построить новую систему множеств, которые также являются событиями. Присоединяя к этим событиям достоверное W и невозможное Æ, получаем систему множеств E, которая является алгеброй, т.е. такой системой подмножеств множества W, что

1) WÎ E,

2) Если АÎ E, то 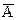Î E,

3) Если АÎ E и ВÎ E, то множества AÈB, AÇB, A\B также принадлежат E.

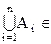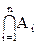Обобщение на n событий: если A_iÎ E, i=1,...,n, то E и Î E.

Таким образом, алгебра – класс множеств, замкнутый относительно конечного числа операций дополнения, объединения и пересечения, а s-алгебра – класс множеств, замкнутый относительно счетного числа этих операций.

Система F множеств А называется s-алгеброй (или борелевским полем событий), если

1) WÎ F;

2) Если АÎ F, то 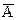Î F;

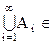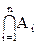3а) Если A_iÎ F,то и F и Î F.

Замечания:

1. В условиях 3) и 3а) достаточно одного утверждения, другое можно получить на основе условия 2) и принципа двойственности.

2. Замкнутость классов E и F позволяет производить соответствующие действия над событиями (множествами), оставаясь в пределах класса.

Если задано пространство элементарных событий W и какая-нибудь алгебра или s - алгебра его подмножеств, то говорят, что задано измеримое пространство (W,E) или (W,F). На измеримом пространстве задается числовая функция P(A), которая называется вероятностью и удовлетворяет трем аксиомам.