Уравнение Майера связывает между собой теплоемкости идеального газа в процессах p=const и v=const. Для удельных теплоемкостей сp и сv эта связь получается из рассмотрения формулы, являющейся определением функции состояния-энтальпии:
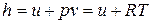 , Дж/кг.
, Дж/кг.
Тогда дифференциал 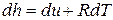 , а производная энтальпии по температуре при
, а производная энтальпии по температуре при 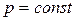 равна:
равна:
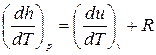 , где R - удельная газовая постоянная, зависящая от рода газа, или
, где R - удельная газовая постоянная, зависящая от рода газа, или 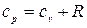 , Дж/кгК, или
, Дж/кгК, или 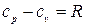 .
.
Для молярных теплоемкостей эта связь имеет вид: 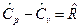 , Дж/мольК, так как
, Дж/мольК, так как 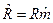 ,
, 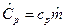 и
и 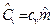 , где
, где 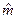 - молярная масса, кг/моль.
- молярная масса, кг/моль.
Для n молей вещества получим связь
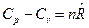 , Дж/К,
, Дж/К,
где n – количество вещества, моль; 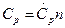 и
и 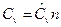 - общие теплоемкости термодинамических процессов при постоянных давлении и объеме соответственно.
- общие теплоемкости термодинамических процессов при постоянных давлении и объеме соответственно.
Отношение изобарной теплоемкости к изохорной теплоемкости называется показателем адиабатного процесса:
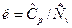 .
.
Для реальных газов показатель к зависит от температуры – к=f (T). Для воздуха и двухатомных газов при 00С показатель к =1,4. С ростом температуры в соответствии с уравнением Майера показатель адиабаты убывает, т.к. теплоемкость 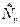 с ростом температуры возрастает:
с ростом температуры возрастает:
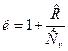 .
.
 2015-01-21
2015-01-21 4141
4141








