I. Общие показатели
1) коэффициент рождаемости показывает число родившихся живыми за год (N) в расчете на 1000 чел. населения определенной территории:
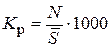 ‰. (7)
‰. (7)
Пример. Среднегодовая численность населения города А составляет 200 тыс. чел. (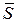 ). За 1999 г. родилось 2,8 тыс. детей (N):
). За 1999 г. родилось 2,8 тыс. детей (N):
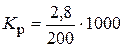 ‰ = 14‰.
‰ = 14‰.
Следовательно, за год в городе родилось 14 детей в расчете на 1000 жителей. Этот показатель уже можно использовать для сравнения уровня рождаемости во временном (для одного и того же населенного пункта) или территориальном аспекте (между разными населенными пунктами).
2) коэффициент смертности показывает число умерших за год (M) в расчете на 1000 чел. населения определенной территории:
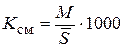 ‰. (8)
‰. (8)
3) коэффициент естественного прироста:
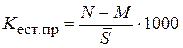 ‰ (9)
‰ (9)
или
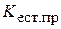 =
= 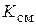 –
– 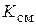 . (10)
. (10)
4) коэффициент жизненности (показатель Покровского)характеризует соотношение между уровнем рождаемости и смертности:
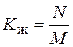 или
или 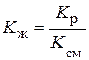 . (11)
. (11)
II. Специальные и частные коэффициенты
1) коэффициент плодовитости (фертильности) (или специальный коэффициент рождаемости) показывает число родившихся за год в расчете на 1000 женщин детородного возраста (возрастная группа 14 – 49 лет):
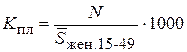 ‰. (12)
‰. (12)
Между общим (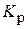 ) и специальным (
) и специальным (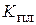 ) коэффициентами рождаемости существует следующая зависимость:
) коэффициентами рождаемости существует следующая зависимость:
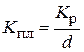 , (13)
, (13)
где 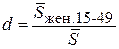 – доля женщин в возрасте 15-49 лет в общей численности населения.
– доля женщин в возрасте 15-49 лет в общей численности населения.
2) возрастные коэффициенты рождаемости и смертности.
а) возрастные коэффициенты смертности определяются как отношение числа умерших за год в возрасте х лет к среднегодовой численности населения данной возрастной группы:
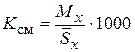 ‰ (14)
‰ (14)
где x – возрастная группа;
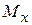 – число умерших за год в возрасте x лет;
– число умерших за год в возрасте x лет;
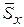 – среднегодовая численность населения данной возрастной
– среднегодовая численность населения данной возрастной
группы.
Т.о., возрастные коэффициенты смертности показывают уровень смертности в отдельной возрастной группе населения (в частности, по формуле (1э-14) могут быть рассчитаны коэффициенты смертности для определенной половой, социальной, профессиональной и иной группы населения (в этом случае х идентифицирует группу населения)).
б) возрастные коэффициенты рождаемости определяются как отношение числа родившихся за год в возрасте х лет к среднегодовой численности населения данной возрастной группы (ср. с п. 2, а):
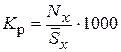 ‰ (15)
‰ (15)
в) суммарные коэффициенты рождаемости показывают число детей, которых родит женщина за весь детородный период; определяется как частное от деления суммы возрастных коэффициентов рождаемости по одногодичным группам на 1000 человек (например, этот коэффициент в 1999 г. в целом по России составил лишь 1,17).
3) коэффициент детской (младенческой) смертности характеризует смертность детей до одного года. Он исчисляется как сумма из двух составляющих: одна из которых – отношение числа умерших в возрасте до одного года из поколения, родившегося в предыдущем году (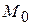 ), к общему числу родившихся в том же периоде (
), к общему числу родившихся в том же периоде (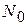 ), а вторая – отношение числа умерших в возрасте до одного года из поколения, родившегося в данном году (
), а вторая – отношение числа умерших в возрасте до одного года из поколения, родившегося в данном году (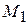 ), к общему числу родившихся в этом же году (
), к общему числу родившихся в этом же году (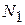 ):
):
 ‰. (16)
‰. (16)
Необходимо особо отметить, что коэффициент детской (младенческой) смертности в международной статистике рассматривается как один из важнейших показателей уровня жизни населения, так вот, эти показатели такие (данные на 1992 г.): Швейцария – 7, США – 9, Россия - 18‰ (!) (для сравнения – в одной их беднейших стран Европы – (в Румынии) этот показатель составляет 23%).
4) показатель средней продолжительности предстоящей жизни для любой возрастной группы населения рассчитывается делением суммы прожитых (предстоящих) человеко-лет жизни 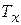 (которые предстоит прожить совокупности лиц от возраста х до предельного возраста включительно) на численность изучаемого поколения (
(которые предстоит прожить совокупности лиц от возраста х до предельного возраста включительно) на численность изучаемого поколения (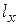 ), дожившего до возраста х:
), дожившего до возраста х:
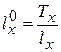 , (17)
, (17)
где 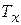 – сумма прожитых (предстоящих) человеко-лет, которые предстоит прожить совокупности лиц от возраста х до предельного возраста включительно, а
– сумма прожитых (предстоящих) человеко-лет, которые предстоит прожить совокупности лиц от возраста х до предельного возраста включительно, а
5) коэффициент оборота населения – число родившихся и умерших на 1000 человек населения в среднем за год:
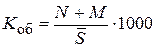 ‰. (18)
‰. (18)
6) коэффициент эффективности воспроизводства населения (как доля естественного прироста в общем обороте населения):
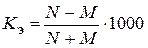 ‰. (19)
‰. (19)
В заключении п. II, что между общими и частными коэффициентами естественного движения населения существует следующая зависимость: общий коэффициент представляет собой среднее из частных коэффициентов. Покажем эту зависимость на примере коэффициентов смертности:
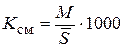 ‰ =
‰ = 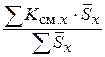 (20)
(20)
Общий коэффициент смертности зависит и от возрастных коэффициентов смертности и от структуры населения. При прочих равных условиях увеличение доли лиц пенсионного возраста (т.е. старения населения) приводит к росту общего коэффициента смертности. Поэтому для сравнительного анализа и динамики демографических процессов возникает необходимость в использовании таких показателей, в которых влияние структурного фактора было бы элиминировано. Для этого рассмотрим п.III.
III. Стандартизированные коэффициенты, которые используются для проведения сравнительного анализа воспроизводства населения по различным территориям или для одной территории в разные моменты времени.
1) коэффициент эффективности воспроизводства населения, который определяется как доля естественного оборота в общем обороте населения:
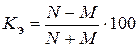 . (21)
. (21)
Пример. Имеются следующие данные по двум населенным пунктам В и С региона в 2009 г.:
Таблица 1
| Возраст, лет | В | С | |||
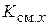 | 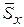 , % к итогу , % к итогу | 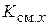 | 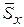 ,% к итогу ,% к итогу | 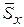 ,5 к итогу ,5 к итогу | |
| 0 – 30 | |||||
| 30 – 60 | |||||
| 60 и ст. | |||||
| Итого | 5,2 | 10,5 |
Из приведенных данных видно, что общий 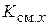 выше в населенном пункте С, хотя возрастные коэффициенты здесь ниже, чем в пункте В. Это связано с различием возрастного состава населения: в населенном пункте С более молодой состав населения. Для устранения влияния структурного фактора рассчитаем стандартизированные показатели (используя, например, данные о возрастном составе населения региона в целом):
выше в населенном пункте С, хотя возрастные коэффициенты здесь ниже, чем в пункте В. Это связано с различием возрастного состава населения: в населенном пункте С более молодой состав населения. Для устранения влияния структурного фактора рассчитаем стандартизированные показатели (используя, например, данные о возрастном составе населения региона в целом):
Для В: 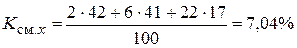 ;
;
Для С: 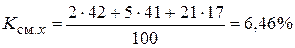 ;
;
Сравнение этих 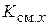 показывает, что уровень смертности выше в населенном пункте В.
показывает, что уровень смертности выше в населенном пункте В.
Т.о., для анализа демографических процессов недостаточно только общих показателей. Полную характеристику воспроизводства населения может дать лишь система взаимосвязанных показателей: общих, частных, специальных, стандартизированных.
 2015-01-21
2015-01-21 4963
4963
