2015-01-21
399
Матрица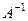 
называется обратной для квадратной матрицы 
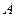, если 
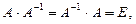где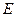 
— единичная матрица.
Любой квадратной матрице 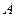можно поставить в соответствие определитель, который обозначается 
.
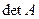Невырожденной называется матрица 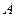, если 
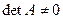. Если матрица невырожденная, то существует единственная обратная ей матрица 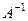, причем,
,
где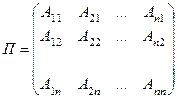 
— присоединенная матрица, 
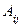— алгебраическое дополнение элемента 
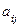матрицы .
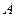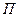Для составления матрицы  следует заменить элементы матрицы 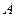соответствующими алгебраическими дополнениями и транспонировать полученную матрицу.
|
Свойства обратной матрицы:
1. 
.
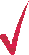
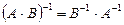2. 
.
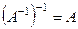3. 
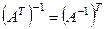
Пример 1.12. Найдите матрицу, обратную к данной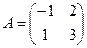 
.
Выполним следующие шаги:
1) Найдём :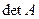 
.
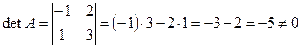Так как 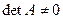, то матрица 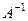существует.
2) Найдём алгебраические дополнения ко всем элементам матрицы :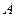
; 
;
; 
.
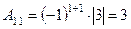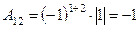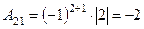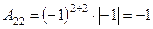3) Запишем матрицу :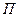
.
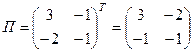4) Найдём матрицу :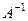
.
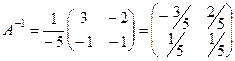Легко проверить, что 
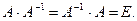
§ 6. Ранг матрицы.
