Некоторые объекты являются рекурсивными по определению, поэтому рекурсивные алгоритмы их получения буквально повторяют соответствующие определения.
Пример: Вычисление факториала натурального числа.
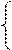 |
|
N(N-1)! При N>1
Function factorial(n:integer): longint;
Begin
if n=1 Then factorial:=1
else factorial:=n*factorial(n-1);
end;
Функция вызывается 5 раз. N=1 - это условие окончания рекурсии.
Задача 2. Написать рекурсивную функцию вычисления значений функции Аккермана для неотрицательных чисел n и m, вводимых с клавиатуры.
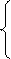 m+1, если n=0
m+1, если n=0
A(n,m) = A(n-1,1), если n¹0, m=0
A(n-1,A(n,m-1)), если n>0, m³0
Задача 3. Найти первые N чисел Фибоначчи. Каждое число Фибоначчи, кроме первых двух, равно сумме двух предыдущих чисел, а первые два равны 1 (1, 1, 2, 3, 5, 8, 13, 21...)
|
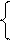 1, если n=1 или n=2
1, если n=1 или n=2 Ф(n-1) + Ф(n-2), если n>2
Задача 4. Найти сумму первых N членов арифметической (геометрической) прогрессии.
 2015-01-21
2015-01-21 1207
1207







