Одной из часто встречающихся практических задач является вычисление корней нелинейного уравнения. В общем случае уравнение имеет вид
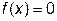 . (21.1)
. (21.1)
Корнем уравнения называется такое значение аргумента х0, при котором это уравнение обращается в тождество. Графически корень уравнения соответствует значению аргумента х0, при котором график функции пересекает ось абсцисс.
Даже в случае обнаружения достаточно узкого участка, содержащего корень уравнения, точное решение можно найти только в исключительных случаях. Численные методы позволяют найти приближенное значение корня. Фактически всегда решается уравнение
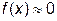 или
или 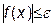 , (21.2)
, (21.2)
где e - некоторая положительная достаточно малая величина. Попытка поиска точного решения или, что то же самое, задание в программе e=0 приводит к зацикливанию вычислительной программы.
Будем считать, что функция f (x) на интервале [ a,b ] непрерывна. При этом функция может не быть гладкой, т.е. содержать изломы, но на этом интервале не должна иметь разрывов.
Задача распадается на несколько отдельных задач:
1) оценить диапазон определения функции (диапазон значений, которые может принимать аргумент);
2) исследовать количество, характер и расположение корней;
3) найти приближенные значения корней;
4) выбрать из них интересующие и вычислить их с требуемой точностью.
Зависимость f (x) может выражаться с помощью системы уравнений и не иметь аналитического вида. Однако и в этом случае мы должны иметь возможность для любого х из допустимого диапазона найти соответствующее ему значение f (x).
Если аналитический вид уравнения известен, то первая задача решается путем анализа вида функции f (x). Например, в уравнении
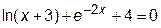
х не может принимать значения, равные или меньше -3, т.к. логарифм нуля и отрицательных чисел не существует.
 2015-01-21
2015-01-21 735
735








