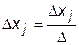 .
.
Здесь D - определитель системы для матрицы, составленной из коэффициентов при неизвестных параметрах; 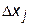 - определитель, в котором столбец коэффициентов при xj заменен на столбец свободных членов bi.
- определитель, в котором столбец коэффициентов при xj заменен на столбец свободных членов bi.
Для системы из трех уравнений использование метода Крамера вызывает некоторые затруднения, для большего количества неизвестных этот метод практически не используется.
Метод Гаусса с выбором главного элемента.
Более эффективным оказывается метод Гаусса, основанный на приведении матрицы коэффициентов к верхнему треугольному виду и последовательному вычислению корней, начиная с хn и заканчивая х1.
Для наглядности рассмотрим конкретную систему из трех уравнений
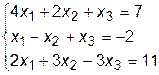 .
.
Так как в вычислениях оперируем только цифрами, то в матрицу запишем только коэффициенты, их индексы будут определяться местом в матрице.
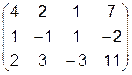 .
.
Известно, что любое уравнение можно умножить на любое число, при этом равенство правой и левой частей не нарушится. Умножим второе уравнение на 4, а третье – на 2. Получим новую матрицу
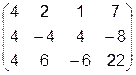 .
.
К каждой части уравнения можно прибавлять или вычитать из нее любое число, равенство частей при этом не изменится. Первое уравнение системы оставим в неизменном виде, а второе и третье заменим разностью между первым и вторым и первым и третьим.
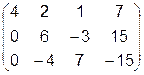 .
.
После этих преобразований получили новую матрицу, в которой за исключением первой строки все коэффициенты в первом столбце равны нулю. Это означает, что соответствующая система уравнений содержит неизвестный параметр х1 только в первом уравнении. Продолжим подобные преобразования для второй строки. Умножим третье уравнение на –3/2. Получим следующую матрицу
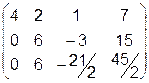 .
.
Далее первую и вторую строку оставим неизменными, а вместо третьей запишем разность между второй и третьей
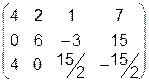 .
.
Эта матрица соответствует системе линейных уравнений
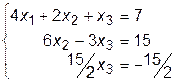 .
.
 2015-01-21
2015-01-21 298
298








