Рассмотрим случай, когда очередная работа начинается сразу после окончания предыдущей работы.
Общее время выполнения системы из n работ
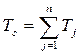 (129)
(129)
Когда случайные величины Тj независимы, плотность распределения φс(t) случайной величины Тс может быть найдена с помощью рекуррентных формул.
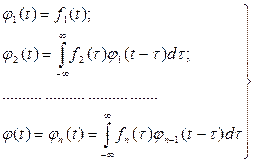 (130)
(130)
где f1(t), f2(t), …, fn(t) – плотность распределения продолжительности выполнения отдельных работ.
Определим функцию распределения (функцию своевременности)
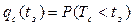 . (131)
. (131)
Используя соотношение (130), получим
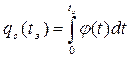 . (132)
. (132)
Перечислим некоторые очевидные свойства функции qc(t):
1) qc(0)=0, т.е.все работы нельзя выполнять мгновенно;
2) qc(t) является неубывающей непрерывной функцией времени;
3) при t→∞ qc(t)→1, т.е. за достаточно большое время работа может быть выполнена любым исполнителем.
Однако практическое применение этих формул в общем случае почти невозможно из-за громоздкости выражений (130).
Надежность системы последовательных работ можно оценить с помощью вероятностного моделирования на ЭВМ.
Для этого с помощью генератора случайного числа имитируются возможные значения времени выполнения каждой работы.
После завершения выполнения последней работы определяется
случайная величина 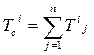 , i-номер запуска на выполнение.
, i-номер запуска на выполнение.
Находится распределение полученных суммарных значений времени 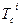 .
.
 2015-01-22
2015-01-22 313
313








