В практике расчета цепей переменного тока широко используются комплексные числа.
Комплексными числами и векторами на комплексной плоскости изображаются изменяющиеся синусоидально ЭДС, ток и напряжение, а также полные сопротивление и проводимость, полная мощность и некоторые другие параметры цепи.
Использование комплексных чисел при расчете электрических цепей переменного тока позволяет заменить графические действия над векторами алгебраическими действиями над комплексными числами. Кроме того, при использовании комплексных чисел возникает полная аналогия записей уравнений по законам Ома и Кирхгофа и методов расчета цепей переменного тока с цепями постоянного тока.
В цепях постоянного тока в уравнения входят действительные значения Е, U, I, r, в цепях переменного тока — комплексные значения U, E, I, Z.
Как известно из курса математики, комплексное число C = a+ jb, где j= 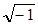 , имеет две составляющие — действительную а и мнимую b, которые являются координатами точки на комплексной плоскости (рис. 2 23, a). Комплексная плоскость представляет собой прямоугольною систему координат. По одной оси. называемой действительной и обозначаемой (+), (—), откладывается действительная составляющая комплекса (a), по другой оси, называемой мнимой и обозначаемой (+j), (-j), — мнимая составляющая комплекса (b).
, имеет две составляющие — действительную а и мнимую b, которые являются координатами точки на комплексной плоскости (рис. 2 23, a). Комплексная плоскость представляет собой прямоугольною систему координат. По одной оси. называемой действительной и обозначаемой (+), (—), откладывается действительная составляющая комплекса (a), по другой оси, называемой мнимой и обозначаемой (+j), (-j), — мнимая составляющая комплекса (b).
Комплексное число обозначается чертой под буквенным обозначением. Комплексное число может быть представлено вектором, длина которого является модулем комплекса, а положение определяется углом α относительно положительной действительной оси комплексной плоскости (рис. 2.23, а).
Выразив а и b через модуль (длину вектора) и угол, можно записать комплексное число в тригонометрической форме:
С = а + jb = с cos α + jc sin α,
где 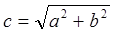 — модуль комплексного числа
— модуль комплексного числа
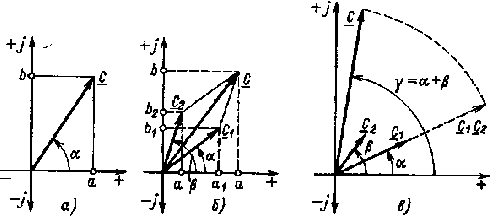
Рис. 2 23 Изображение комплексного числа на комплексной плоскости (а), сложение (б) и умножение (в) комплексов
Согласно формуле Эйлера комплексное число можно записать в показательной форме:
С = сеjα,
где e - основание натуральных логарифмов.
Рассмотрим основные геометрические операции над векторами и алгебраические действия над комплексными числами, их изображающими.
Сложение двух комплексов можно произвести аналитически:
С = С 1+ С 2 = (a1 + jb1) + (a2 + jb2) = (a1 + a2) + j(b1 + b2) = a + jb
или графически по правилу сложения векторов (рис. 2.23, б).
Произведение двух комплексных чисел, изображающих векторы С1 и С2 является комплексным числом, которому соответствует вектор С.
С = С 1 С 2 = с1еjαс2еjβ = c1c2ej(α+β) = сеjγ.
Вектор комплекса произведения двух векторов имеет длину, равную произведению модулей, а его положение относительно действительной положительной оси определяется суммой углов векторов сомножителей (рис. 2.23, в).
Новый вектор, возникающий в результате умножения комплексного числа С = сеjα на +j или -j. имеет тот же модуль с, но повернут на 90° относительно исходного вектора: в одном случае — против часовой стрелки, в другом — по часовой стрелке.
Действительно, векторы +j и -j в показательной форме могут быть записаны следующим образом:
j = 1еj90° = еj90°;
-j = 1е-j90° = е-j90°.
Тогда
C j = сеjαj = сеjαеj90° = cej(α + 90°);
C (-j)= cejα(-j) = сеjαе-j90° = cej(α - 90°).
В результате деления двух комплексных чисел получается комплексное число
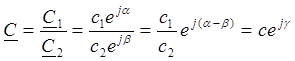
модуль которого равен частному от деления модулей, а угол - разности углов исходных комплексов.
 2015-01-22
2015-01-22 3024
3024
