До сих пор как при рассмотрении вопросов, связанных с ламинарным течением, так и с турбулентным, ничего не говорилось о шероховатости поверхности труб и ее влияния на потерю энергии движущейся жидкости. Однако трубопроводы всегда обладают в той или иной степени неровностями на внутренней поверхности и поэтому не являются гладкими. В гидравлике при решении вопроса о шероховатости стенки играет большую роль ламинарный подслой, или так называемая ламинарная пленка.
Обозначим абсолютный выступ шероховатости через  . Если при движении жидкости в трубе ламинарная пленка полностью покрывает выступы шероховатости, т.е если
. Если при движении жидкости в трубе ламинарная пленка полностью покрывает выступы шероховатости, т.е если 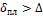 , то, с точки зрения гидравлики, труба рассматривается как гладкая (гидравлически гладкая). Однако с повышением числа Re толщина ламинарной пленки уменьшается. При достижении некоторого значения числа Рейнольдса бугорки шероховатости начнут разрывать ламинарную пленку и, вызывая дополнительные возмущения в потоке, будут влиять на величину потери энергии движущейся жидкости.
, то, с точки зрения гидравлики, труба рассматривается как гладкая (гидравлически гладкая). Однако с повышением числа Re толщина ламинарной пленки уменьшается. При достижении некоторого значения числа Рейнольдса бугорки шероховатости начнут разрывать ламинарную пленку и, вызывая дополнительные возмущения в потоке, будут влиять на величину потери энергии движущейся жидкости.
Обычно, при обработки опытных данных шероховатость определяется не абсолютным значением выступа шероховатости, а отношением его к внутреннему диаметру трубы  . Это относительная шероховатость (степень шероховатости
. Это относительная шероховатость (степень шероховатости 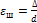 )
)
В области турбулентного течения можно выделить три зоны.
1. Зона гладкостенного сопротивления ( Гидравлически гладкие трубы ) – это зона, в которой коэффициент гидравлического сопротивления зависит только от режима движения 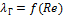 : ламинарный подслой покрывает все выступы. Для таких труб назовем две формулы для нахождения
: ламинарный подслой покрывает все выступы. Для таких труб назовем две формулы для нахождения 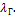
Формула Блазиуса: 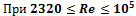
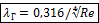
Формула Никурадзе для Re 105 ¸ 3,4×106
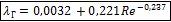
2. Зона шероховатого трения или зона докватратичного сопротивления (гидравлически шероховатые трубы), в которой 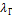 является функцией и режима движения и шероховатости
является функцией и режима движения и шероховатости 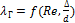 :в некоторых местах таких труб ламинарная пленка, покрывающая выступы в трубе, рвется наиболее высокими выступами шероховатости, и в таких местах образуются вихри.
:в некоторых местах таких труб ламинарная пленка, покрывающая выступы в трубе, рвется наиболее высокими выступами шероховатости, и в таких местах образуются вихри.
Рекомендуется формула Альтшуля для 2320 < Re < 218 × d/D:
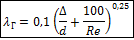
3. Зона вполне шероховатого трения или зона квадратичного сопротивления. (Гидравлически вполне шероховатые трубы) – ламинарная пленка рвется повсюду. Каждый бугорок работает на сопротивление. В данном случае коэффициент гидравлического сопротивления 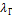 является функцией только шероховатости (автомодельный режим). Рекомендуется формула Шифринсона для Re
является функцией только шероховатости (автомодельный режим). Рекомендуется формула Шифринсона для Re 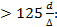
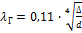
Общий график зависимости 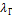 от критерия Рейнольдса и от степени шероховатости показан на рисунке
от критерия Рейнольдса и от степени шероховатости показан на рисунке
Рис. Зависимость коэффициента гидравлического сопротивления от критерия Рейнольдса. 1 – ламинарный режим, формула 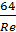 ; 2 – зона гладкостенного сопротивления, формулы Блазиуса и Никурадзе; 3 – зона шероховатого трения, формула Альтшуля; 4 - зона вполне шероховатого трения, формула Шифринсона. ; 2 – зона гладкостенного сопротивления, формулы Блазиуса и Никурадзе; 3 – зона шероховатого трения, формула Альтшуля; 4 - зона вполне шероховатого трения, формула Шифринсона. |
| 2 |
| турб. реж. |
| перех. реж. |
| ламин. реж. |
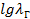 |
 |
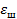 |
| 1 |
| 3 |
| 4 |
В уравнении Бернулли, записанном для потока вязкой жидкости
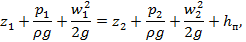
слагаемое 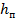 , стоящее в правой части, содержит в себе как потери на трение (путевые потери), так и потери энергии, идущие на преодоление местных сопротивлений.
, стоящее в правой части, содержит в себе как потери на трение (путевые потери), так и потери энергии, идущие на преодоление местных сопротивлений.
Местными сопротивлениями называются сопротивления движению, возникающие в потоках жидкости на участках резкого изменения конфигурации потока, например при резком сопряжении труб различных диаметров, при различного рода поворотах, в местах присоединения вентилей, задвижек, клапанов и т.д.
При прохождении жидкости через участки с местными сопротивлениями энергия жидкости теряется на изменение направления и перераспределение скоростей, на возникающие вихреобразования и срывы потока, сопровождающиеся бурным перемешиванием между частицами жидкости и интенсивном обменом количества движения.
Местные потери энергии вычисляются по формуле
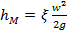 , где
, где 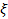 - коэффициент местного сопротивления (справочная величина в зависимости от вида местного сопротивления, геометрических размеров и Re), w – бо'льшая скорость участка местного сопротивления. Если на рассматриваемом участке трубопровода одного диаметра имеется несколько местных сопротивлений, тогда, согласно принципу наложения потерь, местные потери представляют собой сумму
- коэффициент местного сопротивления (справочная величина в зависимости от вида местного сопротивления, геометрических размеров и Re), w – бо'льшая скорость участка местного сопротивления. Если на рассматриваемом участке трубопровода одного диаметра имеется несколько местных сопротивлений, тогда, согласно принципу наложения потерь, местные потери представляют собой сумму
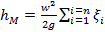 , где n – число местных сопротивлений.
, где n – число местных сопротивлений.
Примечание: принцип наложения потерь справедлив при условии, если местные сопротивления находятся друг от друга на расстоянии не менее 20 диаметров трубы.
Общие потери энергии движущейся жидкости.
Общие потери энергии движущейся жидкости в трубопроводе одного диаметра рассчитываются по формуле
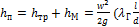 +
+ 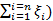 .
.
 2014-10-30
2014-10-30 4796
4796
