Для определения путевых потерь (потерь на трение)
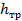
при равномерном течении жидкости в горизонтальном прямом трубопроводе рассматривается участок потока
жидкости в трубопроводе длиной l с произвольной (но постоянной) формой и площадью поперечного cечения f; периметр этого сечения равен П, причем канал полностью заполнен движущейся жидкостью, так что речь идет о смоченном периметре; 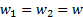 - средняя скорость потока.
- средняя скорость потока.
Итак жидкость движется стационарно (равномерно) слева направо в направлении оси x под действием разности давлений 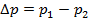 . Исключается из рассмотрения влияние сил тяжести, так как трубопровод горизонтальный. Исключаются из рассмотрения силы инерции, так как по всей длине площадь поперечного сечения постоянна, а форма поперечного сечения произвольна, но также постоянна по всей длине выделенного участка потока. В противоположном направлении движению жидкости действуют касательные напряжения трения. Задача анализа заключается в отыскании функциональной связи между величиной потерянного напора и остальными элементами баланса действующих сил.
. Исключается из рассмотрения влияние сил тяжести, так как трубопровод горизонтальный. Исключаются из рассмотрения силы инерции, так как по всей длине площадь поперечного сечения постоянна, а форма поперечного сечения произвольна, но также постоянна по всей длине выделенного участка потока. В противоположном направлении движению жидкости действуют касательные напряжения трения. Задача анализа заключается в отыскании функциональной связи между величиной потерянного напора и остальными элементами баланса действующих сил.
Анализ будем проводить в терминах баланса действующих сил в соответствии с действительным направлением этих сил относительно оси x (в терминах ОБС направления действующих сил принималось положительным всегда (см. выше). На левое торцевое сечение выделенного цилиндра действует сила давления 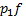 . На правое торцевое сечение – сила давления
. На правое торцевое сечение – сила давления 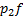 . На боковой поверхности цилиндра действует сила трения между жидкостью и внутренней стенкой трубопровода
. На боковой поверхности цилиндра действует сила трения между жидкостью и внутренней стенкой трубопровода 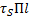 .
.
Поскольку движение является установившимся и равномерным, то силы давления уравновешиваются силами трения, т.е. сумма действующих сил равна 0. Тогда
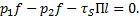
Делим каждый член полученного выражения на 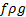 , получаем
, получаем
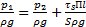 . Преобразуем полученное выражение до вида (добавляя нивелирные и скоростные высоты в двух сечениях потока жидкости)
. Преобразуем полученное выражение до вида (добавляя нивелирные и скоростные высоты в двух сечениях потока жидкости)
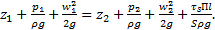 Сравнивая полученное выражение с уравнением Бернулли для реальной жидкости, находят, что
Сравнивая полученное выражение с уравнением Бернулли для реальной жидкости, находят, что
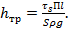 (С другой стороны
(С другой стороны 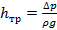 ).
).
Ранее было показано, что эквивалентный диаметр 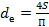 . Делая замену, получают
. Делая замену, получают 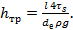
Трудноопределимым в этом выражении является напряжение трения на стенках канала 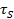 . От него избавляются, подставляя вместо
. От него избавляются, подставляя вместо 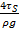 пропорциональную ей иную величину той же размерности. В качестве таковой не следует выбирать
пропорциональную ей иную величину той же размерности. В качестве таковой не следует выбирать 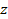 или
или 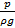 из-за изменения их значений по длине канала. Этот комплекс принимается пропорциональным скоростному напору
из-за изменения их значений по длине канала. Этот комплекс принимается пропорциональным скоростному напору 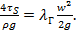 Это удобно, поскольку в каналах постоянного поперечного сечения скорость (средняя) не меняется по его длине. Итак
Это удобно, поскольку в каналах постоянного поперечного сечения скорость (средняя) не меняется по его длине. Итак
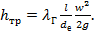 Это выражение называется уравнением равномерного движения или уравнением Дарси-Вейсбаха.
Это выражение называется уравнением равномерного движения или уравнением Дарси-Вейсбаха.
Коэффициент пропорциональности 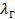 носит название коэффициента гидравлического сопротивления.
носит название коэффициента гидравлического сопротивления.
Для круглых труб в уравнении равномерного движения эквивалентный диаметр заменяется геометрическим, d.
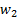
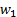
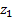
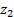
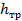 при равномерном течении жидкости в горизонтальном прямом трубопроводе рассматривается участок потока
при равномерном течении жидкости в горизонтальном прямом трубопроводе рассматривается участок потока 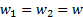 - средняя скорость потока.
- средняя скорость потока.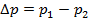 . Исключается из рассмотрения влияние сил тяжести, так как трубопровод горизонтальный. Исключаются из рассмотрения силы инерции, так как по всей длине площадь поперечного сечения постоянна, а форма поперечного сечения произвольна, но также постоянна по всей длине выделенного участка потока. В противоположном направлении движению жидкости действуют касательные напряжения трения. Задача анализа заключается в отыскании функциональной связи между величиной потерянного напора и остальными элементами баланса действующих сил.
. Исключается из рассмотрения влияние сил тяжести, так как трубопровод горизонтальный. Исключаются из рассмотрения силы инерции, так как по всей длине площадь поперечного сечения постоянна, а форма поперечного сечения произвольна, но также постоянна по всей длине выделенного участка потока. В противоположном направлении движению жидкости действуют касательные напряжения трения. Задача анализа заключается в отыскании функциональной связи между величиной потерянного напора и остальными элементами баланса действующих сил.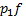 . На правое торцевое сечение – сила давления
. На правое торцевое сечение – сила давления 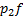 . На боковой поверхности цилиндра действует сила трения между жидкостью и внутренней стенкой трубопровода
. На боковой поверхности цилиндра действует сила трения между жидкостью и внутренней стенкой трубопровода 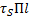 .
.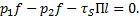
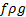 , получаем
, получаем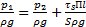 . Преобразуем полученное выражение до вида (добавляя нивелирные и скоростные высоты в двух сечениях потока жидкости)
. Преобразуем полученное выражение до вида (добавляя нивелирные и скоростные высоты в двух сечениях потока жидкости)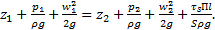 Сравнивая полученное выражение с уравнением Бернулли для реальной жидкости, находят, что
Сравнивая полученное выражение с уравнением Бернулли для реальной жидкости, находят, что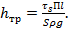 (С другой стороны
(С другой стороны 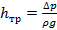 ).
).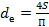 . Делая замену, получают
. Делая замену, получают 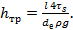
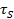 . От него избавляются, подставляя вместо
. От него избавляются, подставляя вместо 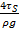 пропорциональную ей иную величину той же размерности. В качестве таковой не следует выбирать
пропорциональную ей иную величину той же размерности. В качестве таковой не следует выбирать 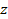 или
или 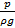 из-за изменения их значений по длине канала. Этот комплекс принимается пропорциональным скоростному напору
из-за изменения их значений по длине канала. Этот комплекс принимается пропорциональным скоростному напору 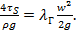 Это удобно, поскольку в каналах постоянного поперечного сечения скорость (средняя) не меняется по его длине. Итак
Это удобно, поскольку в каналах постоянного поперечного сечения скорость (средняя) не меняется по его длине. Итак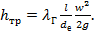 Это выражение называется уравнением равномерного движения или уравнением Дарси-Вейсбаха.
Это выражение называется уравнением равномерного движения или уравнением Дарси-Вейсбаха.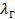 носит название коэффициента гидравлического сопротивления.
носит название коэффициента гидравлического сопротивления. 2014-10-30
2014-10-30 1727
1727
