При расчете простого трубопровода решают две задачи:
1. Задача проектирования:
Дано H, V, l.
Найти: диаметр трубопровода.
2. Задача эксплуатации:
Дано l, d, H(V).
Найти V(H).
| 0 |
| P1 |
| f1 |
| w1 |
| P2 |
| f2 |
| w2 |
| w |
| V |
| V |
| z2 |
| z1 |
| l, d, lГ |
| h |
| f |
| 0 |
Чтобы вывести формулу для решения любой из поставленных задач, воспользуемся уравнением Бернулли для вязкой жидкости:
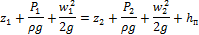
дополняем уравнением сплошности:
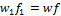
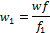
отношение f/f1» 0, так как Sтруб-да<<S1. Отсюда следует, что w1 » 0. Это значит что и
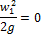
тоже самое и с w2:
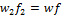
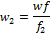
отношение f/f2» 0, так как fтруб-да<<f2. Отсюда следует, что w2 » 0. Это значит что и
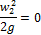
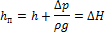
Правую часть уравнения называют суммарный располагаемый гидростатический напор (DH).
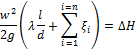
Итак, получаем первую основную формулу для расчета простого трубопровода:
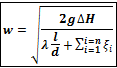
где n – число местных сопротивлений.
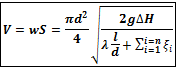
Пусть p1 = p2, тогда DH = h – высота “подъема” жидкости (расстояние между первым и вторым сечениями потока жидкости).
Алгоритм расчета задачи проектирования:
1. Задаемся скоростью жидкости в трубопроводе
w
2. Определяем диаметр из уравнения расхода (искомая величина – диаметр)
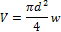
3. Расчет режима движения жидкости
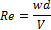
4. Выбор расчетной формулы для lГ: для гидравлически гладких труб формула Никурадзе или Блазиуса.
5. Расчет lГ по выбранной формуле.
6. Расчет скорости жидкости в трубе.
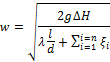
7.Сопоставление (C) w(6п) и w(1п)
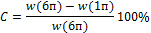
если С < 0,1%, то d = d(в первом приближении)
если С > 0,1%, то возвращаемся в первый пункт, при этом используем результат первого приближения по скорости; и т.д.
 2014-10-30
2014-10-30 782
782








