Среди реологически стационарных есть группа жидкостей, которые не движутся при относительно небольших приложенных усилиях. Движение начинается только при напряжениях, превышающих предельную величину t0, называемую пределом текучести. При 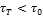 нет относительного сдвига слоев жидкости:
нет относительного сдвига слоев жидкости: 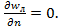 Внутри этой группы есть жидкости, которые при
Внутри этой группы есть жидкости, которые при 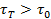 под действием избытка напряжений
под действием избытка напряжений 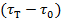 ведут себя как ньютоновские. Для них уравнение сдвига имеет вид
ведут себя как ньютоновские. Для них уравнение сдвига имеет вид
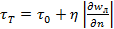 , где
, где 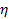 называется коэффициентом пластической вязкости. Такие жидкости получили название бингамовских (густые мелкодисперсные суспензии, пасты, некоторые шламы). Из рисунка б) видно, что с увеличением
называется коэффициентом пластической вязкости. Такие жидкости получили название бингамовских (густые мелкодисперсные суспензии, пасты, некоторые шламы). Из рисунка б) видно, что с увеличением 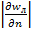 величина
величина 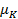 уменьшается. В самом деле, сопоставим выражения
уменьшается. В самом деле, сопоставим выражения 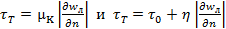 , приравняв правые части.
, приравняв правые части.
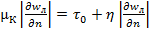 , откуда
, откуда 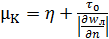 .
.
Из полученного выражения следует, что с ростом градиента скорости уменьшается кажущаяся вязкость и при 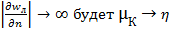 , т.е. при больших приложенных усилиях бингамовская жидкость начинает вести себя как ньютоновская (с постоянной вязкостью).
, т.е. при больших приложенных усилиях бингамовская жидкость начинает вести себя как ньютоновская (с постоянной вязкостью).
Среди стационарных есть группа жидкостей, уравнение сдвига которых может быть представлено в виде степенной зависимости 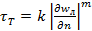 , где k и m – эмпирически подобранные константы, характерные для данной жидкости. Жидкости, для которых
, где k и m – эмпирически подобранные константы, характерные для данной жидкости. Жидкости, для которых 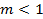 , - псевдопластичные жидкости (низкомолекулярные полимеры, некоторые суспензии). Как видно из рисунка в) кажущаяся вязкость уменьшается с увеличением градиента скорости. В самом деле, сопоставим два выражения
, - псевдопластичные жидкости (низкомолекулярные полимеры, некоторые суспензии). Как видно из рисунка в) кажущаяся вязкость уменьшается с увеличением градиента скорости. В самом деле, сопоставим два выражения
и 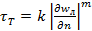 , приравняв правые части этих выражений.
, приравняв правые части этих выражений.
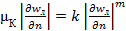 , откуда
, откуда 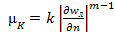 . Поскольку
. Поскольку 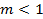 , то с ростом градиента скорости величина
, то с ростом градиента скорости величина 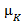 уменьшается.
уменьшается.
| Рис. в. Диаграмма сдвига для псевдопластичной жидкости.
|
| Рис. г. Диаграмма сдвига для дилатантной жидкости.
|
Жидкости, для которых 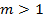 , носит название дилатантных (густые суспензии, замешанные на невязких жидкостях, клеи); диаграмма сдвига для них изображена на рисунке г). Кажущаяся вязкость для них увеличивается с ростом градиента скорости, как следует из рисунка г). Аналитически это подтверждается согласно выражения
, носит название дилатантных (густые суспензии, замешанные на невязких жидкостях, клеи); диаграмма сдвига для них изображена на рисунке г). Кажущаяся вязкость для них увеличивается с ростом градиента скорости, как следует из рисунка г). Аналитически это подтверждается согласно выражения
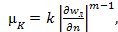 с ростом градиента скорости кажущаяся вязкость растет, поскольку
с ростом градиента скорости кажущаяся вязкость растет, поскольку 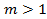
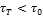 нет относительного сдвига слоев жидкости:
нет относительного сдвига слоев жидкости: 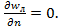 Внутри этой группы есть жидкости, которые при
Внутри этой группы есть жидкости, которые при 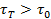 под действием избытка напряжений
под действием избытка напряжений 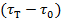 ведут себя как ньютоновские. Для них уравнение сдвига имеет вид
ведут себя как ньютоновские. Для них уравнение сдвига имеет вид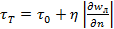 , где
, где 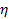 называется коэффициентом пластической вязкости. Такие жидкости получили название бингамовских (густые мелкодисперсные суспензии, пасты, некоторые шламы). Из рисунка б) видно, что с увеличением
называется коэффициентом пластической вязкости. Такие жидкости получили название бингамовских (густые мелкодисперсные суспензии, пасты, некоторые шламы). Из рисунка б) видно, что с увеличением 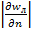 величина
величина 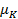 уменьшается. В самом деле, сопоставим выражения
уменьшается. В самом деле, сопоставим выражения 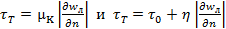 , приравняв правые части.
, приравняв правые части.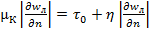 , откуда
, откуда 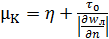 .
.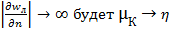 , т.е. при больших приложенных усилиях бингамовская жидкость начинает вести себя как ньютоновская (с постоянной вязкостью).
, т.е. при больших приложенных усилиях бингамовская жидкость начинает вести себя как ньютоновская (с постоянной вязкостью).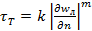 , где k и m – эмпирически подобранные константы, характерные для данной жидкости. Жидкости, для которых
, где k и m – эмпирически подобранные константы, характерные для данной жидкости. Жидкости, для которых 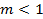 , - псевдопластичные жидкости (низкомолекулярные полимеры, некоторые суспензии). Как видно из рисунка в) кажущаяся вязкость уменьшается с увеличением градиента скорости. В самом деле, сопоставим два выражения
, - псевдопластичные жидкости (низкомолекулярные полимеры, некоторые суспензии). Как видно из рисунка в) кажущаяся вязкость уменьшается с увеличением градиента скорости. В самом деле, сопоставим два выражения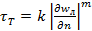 , приравняв правые части этих выражений.
, приравняв правые части этих выражений.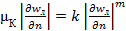 , откуда
, откуда 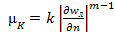 . Поскольку
. Поскольку 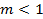 , то с ростом градиента скорости величина
, то с ростом градиента скорости величина 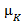 уменьшается.
уменьшается.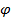
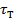
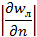
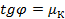
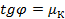
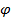
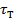
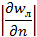
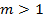 , носит название дилатантных (густые суспензии, замешанные на невязких жидкостях, клеи); диаграмма сдвига для них изображена на рисунке г). Кажущаяся вязкость для них увеличивается с ростом градиента скорости, как следует из рисунка г). Аналитически это подтверждается согласно выражения
, носит название дилатантных (густые суспензии, замешанные на невязких жидкостях, клеи); диаграмма сдвига для них изображена на рисунке г). Кажущаяся вязкость для них увеличивается с ростом градиента скорости, как следует из рисунка г). Аналитически это подтверждается согласно выражения 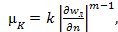 с ростом градиента скорости кажущаяся вязкость растет, поскольку
с ростом градиента скорости кажущаяся вязкость растет, поскольку 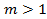
 2014-10-30
2014-10-30 349
349







