Упругие свойства пород

Для упругих пород (упругих деформаций) связи между напряжениями и деформациями – линейные и выражаются обобщенным законом Гука, который для изотропных тел имеет вид следующих шести равенств:

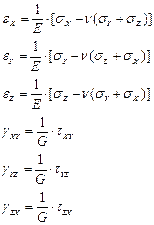(2.4)

(2.5)

(2.6)

(2.7)

(2.8)

(2.9)

куда входят три параметра упругости: Е – модуль продольной упругости (модуль Юнга); G – модуль сдвига, n - коэффициент Пуассона.
Физический смысл этих параметров очевиден из приведенных выше уравнений (закон Гука).

1. Из первых трех уравнений при n = 0 имеем:

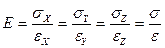
т.е. при , .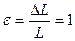

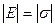Это значит, что численно модуль Юнга lEl равен напряжению lsl, при котором длина образца L увеличивается в 2 раза (т.е. DL=L).

Модуль Юнга для горных пород, как правило, лежит а пределах 10⁹ – 10¹¹ Па.

2. модуль сдвига G - коэффициент пропорциональности между касательным напряжением t и соответствующей упругой деформацией сдвига g:

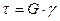
При g =1 (радиан) , т.е. численно модуль сдвига G равен касательному напряжению t, вызывающему поворот соответствующей грани элемента на угол в 1 радиан.

3. коэффициент Пуассона n - это отношение относительного поперечного сокращения 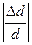образца к его относительному удлинению 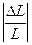при действии нормального напряжения по направлению L (рис.2.2а), т.е.

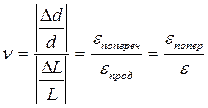
так как тело при сжатии расширяется, а при растяжении – сужается, то

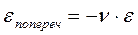
т.е. поперечная деформация e_{попереч} составляет часть продольной.

Коэффициент Пуасона n для горных пород изменяется, как правило, в пределах 0¸0.5. Из трех параметров (Е, G, n) упругости независимых только два, т.к. между ними существует формула связи:

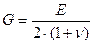
В случае равномерного трехосного сжатия упругого тела наблюдается прямая пропорциональность между давлением Р₀ и относительным изменением объема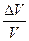

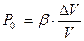
где b - модуль объемного (всестороннего) сжатия.

Модуль объемного сжатия пород b выражается через выше приведенные упругие параметры пород:

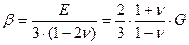
В качестве примера рассмотрим распределение напряжений в горном массиве для простейшего случая однородных и изотропных горных пород (нормальное поле напряжений, не искаженное бурением скважин).

В условиях равновесия внешнее давление под действием веса вышележащих пород равно возникающим ответным напряжениям в породе:

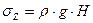
где s_Z – вертикальная составляющая напряжений, r - плотность пород (r = const), g – ускорение свободного падения, Н – глубина залегания пласта.

По горизонтали (в рассматриваемом простейшем случае):

(а)

где n – коэффициент бокового распора (). (б)

Для пластичных и жидких пород типа плывунов (когда напряжения определяются гидростатическим законом) n=1.

Для плотных и крепких пород (вне зон тектонических напряжений n<1 – доли единицы). Для хрупких пород h~0.3¸0.7

Оценим приближение коэффициента бокового распора n и горизонтального напряжения пород s_X=s_Y:

Выделим элементарный объем. Его относительная деформация по оси х - e_X определяется выражением (2.4):

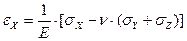
С учетом (а) и (б) имеем:

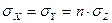
Предположим, что при осадконакоплении происходит только сжатие пород в вертикальном направлении, а деформации в горизонтальном направлении не было:

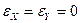
Тогда из (1) находим:

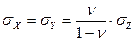
т.е. сравнивая с (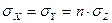), находим:

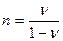
Это значит, что при 0 £n < 0,5 0 £ n <1 и горизонтальные напряжения в породах меньше вертикальных (что обычно бывает на небольших глубинах при отсутствии пластичных пород, у которых n=1)

При больших давлениях и глубинах (более 2500 – 3000 м) может происходить выравнивание напряжений вплоть до гидростатических, т.к. за длительные периоды времени породы испытывают пластические или псевдопластические деформации.

Однако, тектонические процессы могут привести к тому, что горизонтальные напряжения могут превышать в 2 – 3 раза вертикальное горное давление.