2015-01-30
543
Основные уравнения теории упругости:
Выделяют три группы уравнений:
1. Статические уравнения, которые отражают условия равновесия (например, элементарного параллелепипеда dx,dy,dz в декартовой системе координат);
2. Геометрические уравнения, связывающие деформации элемента тела с перемещениями его точек U, V, W соответственно по координатам x, y,z;
3. Физические уравнения, учитывающие механические свойства горных пород (для упругих пород – это обобщенный закон Гука).
Для сплошных однородных и изотропных горных пород имеем:
1. Статические уравнения:
а) Приравнивая сумму проекций всех сил на оси x, y,z последовательно:
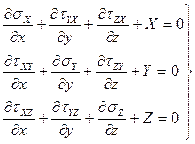(2.15)
где X, Y, Z – составляющие интенсивности (т.е. отнесенной к единице объема) объемной внешней нагрузки (например, веса тела или силы инерции)
б) приравнивая нулю сумму моментов всех сил относительно осей x, y,z получим известный закон парности касательных напряжений:
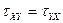
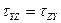
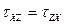(2.16)
2. Геометрические уравнения:
а) вытекающий из определения деформаций (уравнения Коши):
|
|
|
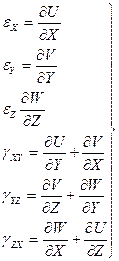(2.17)
б) вытекающие из условия сплошности (неразрывности) среды – уравнения совместности деформаций:
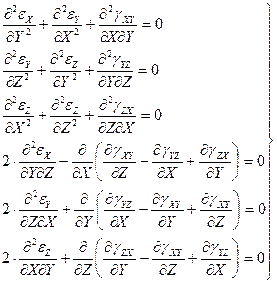(2.18)
3. Физические уравнения (обобщенный закон Гука для линейно-упругих изотропных тел):
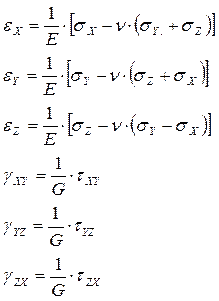(2.19)
где Е – модуль Юнга (модуль продольной упругости); G – модуль сдвига; n - коэффициент Пуассона.
Имеем два основных метода (способа) решения уравнений (2.15) – (2.19):
1. метод напряжений;
2. метод перемещений.
В методе напряжений за основные неизвестные функции принимают шесть функций напряжений (sX, sY, sZ, tXY, tYZ, tZX). Для постоянной объемной силы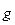 
(X, Y, Z)=const из уравнений совместности с использованием уравнений Гука и уравнения равновесия получают для них следующую систему уравнений (уравнений Бельтрами):
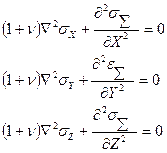
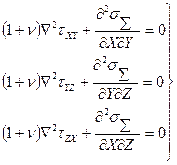(2.20)
где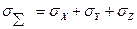 
, 
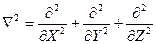- оператор Лапласа.
Найдя из шести уравнений шесть неизвестных функций sX, sY, sZ, tXY, tYZ, tZX, затем из уравнений закона Гука находим деформации, а интегрирую уравнения Коши – перемещение (при соответствующих граничных условий).,
В методе перемещений за основные неизвестные принимаются три функции – перемещения U, V, W точек тела по координатам x, y, z соответственно, а в качестве разрешающих – три уравнения равновесия (2.15), которые с учетом закона Гука и геометрических уравнений дают три уравнения равновесия, выраженные через перемещения (уравнение Ламе):
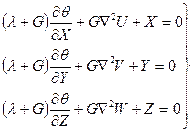(2.21)
где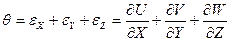 
, 
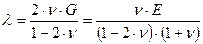- параметр Ламе (2.22) G – модуль сдвига.
Граничные условия для уравнения (2.21) формулируют, например, приравнивая функции U, V, W на границе заданной перемещениям (если рассматриваемая деформация тела вызывается заданными принудительными перемещениями его поверхности.
Если же на поверхность тела действует заданная поверхностная нагрузка р, то предварительно в уравнениях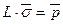 
заменить напряжения s через перемещения U по известной разработанной схеме.
|
|
|
Обобщенный закон Гука – формулы (2.4) – (2.5) для плоской задачи (sZ=0, eZ=0):
1. в декартовых координатах (x, y) имеет вид:
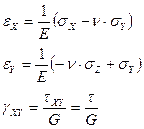
где sX, sY – нормальные напряжения по осям х и y соответственно; tXY – касательное напряжение в плоскости х,у; eX, eY – относительные деформации по осям х и у соответственно; Е – модуль Юнга; n - коэффициент Пуассона;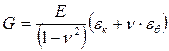 
; 
; 
.
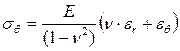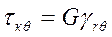В полярных координатах связь между перемещениями (по оси r – U) и (по оси q - V) и между соответствующими относительными деформациями er, eq, grq имеют вид:
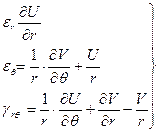
Статические уравнения. Эти уравнения выражают равенство нулю сумм проекций всех сил, действующих на элемент (d2, d3) на радиальные направления r и на перпендикулярное ему тангенциальное направление dS(q):
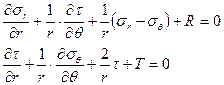
где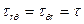 
R и T – компоненты *радиальная и тангенциальная) внешних объемных нагрузок.
