В плоском криволинейном стержне так же, как в плоской раме, состоящей из прямолинейных стержней, возникает три внутренних усилия: N, Q и М. Процесс определения внутренних усилий в криволинейном стержне тот же, что и в раме. Особенность состоит в новом правиле знаков для изгибающего момента: изгибающий момент считается положительным, если он увеличивает кривизну стержня (Если рассматриваемый стержень имеет и прямолинейный, и криволинейный участки, то для того, чтобы не было противоречия из-за разного правила знаков для изгибающего момента в прямолинейной и криволинейной частях стержня, принято строить эпюру изгибающего момента со стороны растянутых волокон без определения знака). Правила знаков для продольной и поперечной сил те же, что и при их определении в плоских рамах.
Построение эпюр внутренних усилий рассмотрим на конкретном примере плоской круговой балки (т. е. балки с осью, очерченной по дуге окружности), изображенной на рис. 3, а.
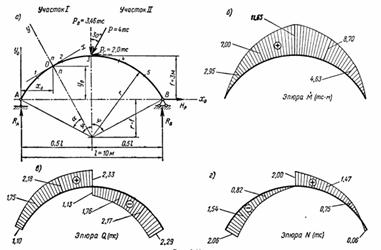
Рис. 3
Для определения опорных реакций составим уравнения равновесия:
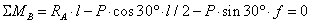 ,
,
откуда
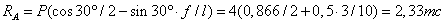 ;
;
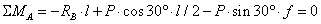 ,
,
откуда
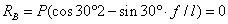 ;
;
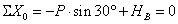 ,
,
откуда
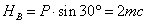
В этих выражениях величины 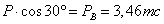 и
и 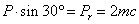 представляют собой соответственно вертикальную и горизонтальную составляющие силы Р; ось
представляют собой соответственно вертикальную и горизонтальную составляющие силы Р; ось 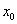 горизонтальна.
горизонтальна.
Определяем значение радиуса r оси балки и центрального угла 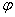 . Из рис. 3, а:
. Из рис. 3, а:
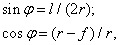
следовательно,
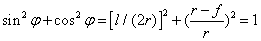 ,
,
откуда
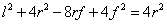
и
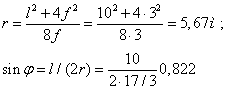
и 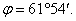
Проведем через произвольную точку О участка 1 балки поперечное сечение n-n. Положение этого сечения определяется углом 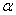 (рис.3, а). С сечением n-n совместим ось у подвижной системы координат; ось х перпендикулярна ей и касательна к оси балки в точке О. Координаты точки О в неподвижной системе координат х 0 у 0 равны:
(рис.3, а). С сечением n-n совместим ось у подвижной системы координат; ось х перпендикулярна ей и касательна к оси балки в точке О. Координаты точки О в неподвижной системе координат х 0 у 0 равны:
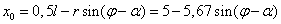 ;
;
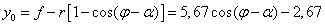 .
.
Составим выражения изгибающего момента 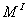 , поперечной силы
, поперечной силы 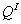 и продольной силы
и продольной силы 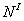 в поперечных сечениях участка I балки:
в поперечных сечениях участка I балки:
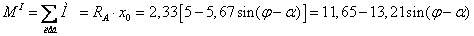 ;
;
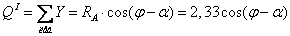 ;
;
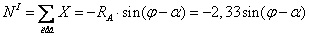 .
.
Аналогично составим выражения 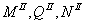 для участка II балки:
для участка II балки:
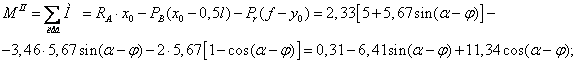
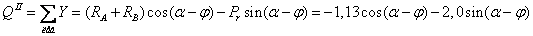 ;
;
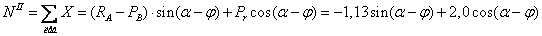 .
.
По полученным значениям усилий в поперечных сечениях балки на рис. 3, б, в, г построены эпюры М, Q и N.
Связь между усилиями М, Q и N, действующими в поперечных сечениях кривого бруса, определяется следующими дифференциальными зависимостями:
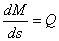 ; (1)
; (1)
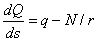 ; (2)
; (2)
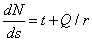 . (3)
. (3)
где q и t — интенсивности распределенных нагрузок соответственно перпендикулярной и параллельной оси бруса; ds - длина элементарного отрезка оси кривого бруса.
Формула (1) аналогична формуле Журавского для прямых брусьев.
Зависимости (1) - (3) могут использоваться для проверки построенных эпюр М, Q и N. Проверим с их помощью эпюры, изображенные на рис. 3.
На участке I балки (см. рис. 3, а) ординаты эпюры Q положительны, а на участке II — отрицательны. Поэтому в соответствии с зависимостями (1) и (3) значения М и N на участке I возрастают слева направо (т.е. с увеличением криволинейной координаты s), а на участке II — убывают. Ординаты эпюры N на участке I отрицательны, а на участке II — положительны; в соответствии с зависимостью (2) значения Q на участке I возрастают, а на участке II — убывают.
Производная 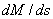 на отрезке, например, 2-3 оси балки (см. рис. 3, а) имеет среднее значение, равное (см. рис.3, 6)
на отрезке, например, 2-3 оси балки (см. рис. 3, а) имеет среднее значение, равное (см. рис.3, 6)
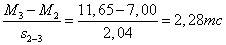 ,
,
где длина участка
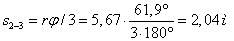 .
.
Этому среднему значению производной в соответствии с зависимостью (1) примерно равна средняя величина Q на отрезке 2-3 (см. рис. 3, в). Производная 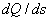 на участке, например, 3-4балки имеет среднее значение
на участке, например, 3-4балки имеет среднее значение
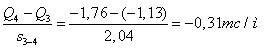 .
.
В соответствии с зависимостью (2) такое же примерно значение на отрезке 3-4 имеет среднее отношение 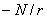 , равное
, равное
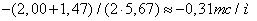 .
.
Аналогично можно проверить выполнение условий (1)-(3) и на других отрезках оси балки.
 2015-01-30
2015-01-30 1854
1854







