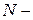 число циклов нагружения до разрушения материала. Видно, что чем меньше
число циклов нагружения до разрушения материала. Видно, что чем меньше 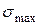 , тем больше циклов выдержит материал. Для
, тем больше циклов выдержит материал. Для стали кривая стремится к асимптоте при 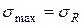 , которую называют пределом выносливости. Это напряжение, при котором не происходит усталостного разрушения данного материала после произвольно большого числа циклов (обычно берут
, которую называют пределом выносливости. Это напряжение, при котором не происходит усталостного разрушения данного материала после произвольно большого числа циклов (обычно берут 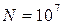 циклов).
циклов).
С помощью кривых Вёлера определяют срок службы элементов конструкций при действии переменных напряжений, возникающих при колебаниях.
На величину предела выносливости влияют многие факторы:
Концентрация напряжений. Она возникает в точках тела вблизи мест приложения сосредоточенных сил, около выточек, у краев отверстий, в местах резкого изменения формы тела, у надрезов и т.д. Концентрация значительно снижает предел выносливости.
Качество поверхности детали. Снижение предела выносливости тем больше, чем грубее поверхностная обработка детали, причем это снижение более значительно для материалов с высокими пределами прочности.
Абсолютные размеры детали. С увеличением размеров предел выносливости уменьшается. Объясняют это тем, что в больших деталях с большим объемом материала больше дефектных мест (раковины, микротрещины, неметаллические включения, следы от обработки поверхности).
Внешняя среда. Коррозионная среда (вода, соленая вода, кислоты, пары и т.д.) резко снижают усталостную прочность. Желательно использовать защитные покрытия поверхностей (окраска, цинкование, азотирование и т.д.)
- Учет сил инерции. Продольный и поперечный удар.
I. Учет сил инерции
Величина элементарной силы инерции 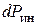 , действующей на частицу тела равна
, действующей на частицу тела равна
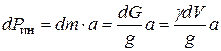 (9.1)
(9.1)
Здесь: 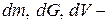 масса, вес, объем частицы;
масса, вес, объем частицы; 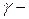 объемный вес материала частицы;
объемный вес материала частицы; 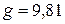 м/сек2 - ускорение свободного падения;
м/сек2 - ускорение свободного падения; 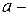 ускорение при движении частицы.
ускорение при движении частицы.
Сила инерции направлена в сторону, противоположную направлению ускорения.
При расчете стержневых конструкций объемные силы инерции удобно представить распределенной погонной инерционной нагрузкой 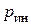 .
.
Стержень длиной 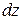 и площадью поперечного сечения А имеет объем
и площадью поперечного сечения А имеет объем 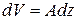 . Подставим это в (9.1)
. Подставим это в (9.1)
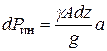
Погонная нагрузка – это нагрузка на единицу длины
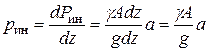 (9.2)
(9.2)
Пример 1. Подъем груза на длинном тросе с постоянным ускорением а.
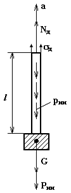 | Дано: 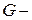 вес груза, вес груза, 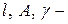 длина, площадь сечения троса и его объемный вес. В сечении троса на расстояние длина, площадь сечения троса и его объемный вес. В сечении троса на расстояние 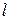 от груза возникает от груза возникает 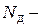 динамическая сила, которая должна уравновешивать: динамическая сила, которая должна уравновешивать: 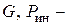 инерционную силу от груза, инерционную силу от груза, 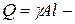 вес троса и вес троса и 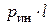 погонную инерционную нагрузку от троса. С учетом (9.1) и (9.2) получим погонную инерционную нагрузку от троса. С учетом (9.1) и (9.2) получим 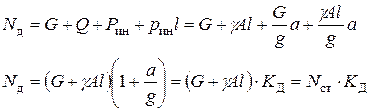 (1) (1) |
Здесь: 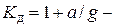 динамический коэффициент,
динамический коэффициент, 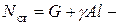 статическое усилие в сечении троса.
статическое усилие в сечении троса.
Обозначим: 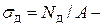 динамическое напряжение,
динамическое напряжение, 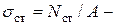 статическое напряжение в тросе.
статическое напряжение в тросе.
Поделив (1) на 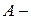 получим
получим
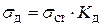
Условие прочности троса 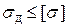 , где
, где 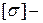 допускаемое напряжение.
допускаемое напряжение.
Пример 2. Вращение стержня в горизонтальной плоскости.
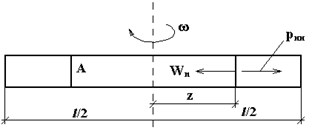 | Дано: 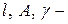 длина, пло-щадь сечения, объемный вес материала стержня; длина, пло-щадь сечения, объемный вес материала стержня; 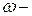 угловая скорость вращения. На расстояние угловая скорость вращения. На расстояние 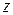 от оси вращения выделим произвольное от оси вращения выделим произвольное |
сечение. При равномерном вращении стержня центростремительное ускорение 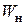 , действующие на частицы стержня в этом сечении, определяется по правилам кинематики
, действующие на частицы стержня в этом сечении, определяется по правилам кинематики 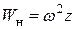 , а погонная инерционная центробежная нагрузка
, а погонная инерционная центробежная нагрузка 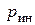 направлена от оси вращения и по (9.2) равна
направлена от оси вращения и по (9.2) равна
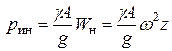 (2)
(2)
Инерционные силы вызывают растяжение стержня силой 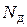 в сечении
в сечении 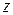 стержня. Т.к
стержня. Т.к 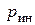 линейно меняется по длине стержня (
линейно меняется по длине стержня (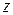 в первой степени в (2)), то
в первой степени в (2)), то 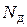 найдем суммированием (интегрированием)
найдем суммированием (интегрированием) 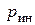 на участке от
на участке от 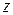 до
до 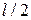
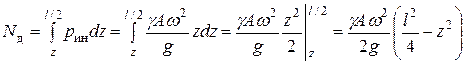 (3)
(3)
Из (3) видно, 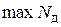 при
при 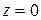 (в середине стержня)
(в середине стержня)
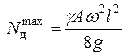 (4)
(4)
Далее можно найти 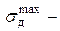 максимальное напряжение в стержне и записать условие его прочности.
максимальное напряжение в стержне и записать условие его прочности.
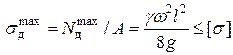 (5)
(5)
Из (5) можно найти max допускаемую скорость вращения 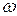 стержня.
стержня.
II. Расчеты на удар тел
Продолжительность удара очень мала и сложно вычислить ускорения частиц ударяемой конструкции. Поэтому, воспользоваться принципом Д¢Аламбера затруднительно и обычно здесь используют закон сохранения энергии.
Для удобства расчета на удар вводят условное понятие динамическая сила 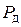 . Эта такая сила, которая, будучи статически приложенной в точке удара, вызовет такие же перемещения (деформации) ударяемого тела, как и при ударе.
. Эта такая сила, которая, будучи статически приложенной в точке удара, вызовет такие же перемещения (деформации) ударяемого тела, как и при ударе.
Расчет на удар без учета массы ударяемого бруса
Рассмотрим закрепленный упругий брус, на который с высоты 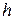 падает груз весом
падает груз весом 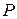 . При этом брус может испытывать: а) продольные деформации (колонны, сваи) рис. 9.1а, б) изгибные деформации (балки) рис. 9.1б.
. При этом брус может испытывать: а) продольные деформации (колонны, сваи) рис. 9.1а, б) изгибные деформации (балки) рис. 9.1б.
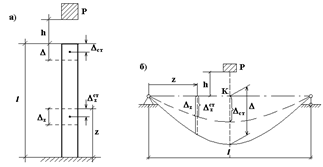
Рис. 9.1
После удара, когда груз 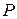 останавливается в нижнем положении, деформации каждого сечения бруса достигают наибольших значений. Их обозначим:
останавливается в нижнем положении, деформации каждого сечения бруса достигают наибольших значений. Их обозначим: 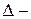 деформации в точке удара,
деформации в точке удара, 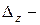 в любом сечении бруса с координатой
в любом сечении бруса с координатой 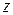 (на рис. 9.1б в эти деформации (прогибы) показаны сплошной линией). Затем происходят затухающие колебания бруса, в конце которых устанавливаются деформации
(на рис. 9.1б в эти деформации (прогибы) показаны сплошной линией). Затем происходят затухающие колебания бруса, в конце которых устанавливаются деформации 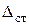 (в точке удара) и
(в точке удара) и 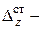 в любом сечении, соответствующие статическому действию груза
в любом сечении, соответствующие статическому действию груза 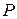 (на рис. 9.1б эти деформации показаны пунктирной линией).
(на рис. 9.1б эти деформации показаны пунктирной линией).
Расчет проведем при следующих допущениях:
4. Брус идеально упругий, справедлив закон Гука, модуль 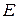 одинаков при динамическом и статическом нагружении;
одинаков при динамическом и статическом нагружении;
5. Массу ударяемого бруса пока не учитываем;
6. Эпюра перемещений сечений бруса от удара подобна эпюре перемещений от статического действия груза 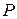 . (На рис. 9.1б графики прогибов, обозначенные сплошной и пунктирной линиями, подобны). Обозначим
. (На рис. 9.1б графики прогибов, обозначенные сплошной и пунктирной линиями, подобны). Обозначим
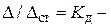 динамический коэффициент (9.3)
динамический коэффициент (9.3)
Из третьего допущения и рис. 9.1б следует с учетом (9.3)
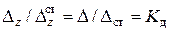 (9.4)
(9.4)
Согласно принятого выше определения динамической силы 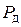 , от ее статического приложения возникнут деформации D и
, от ее статического приложения возникнут деформации D и 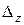 , а от статического нагружения силой
, а от статического нагружения силой 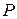 появятся
появятся 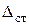 и
и 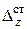 . По закону Гука деформации пропорциональны нагрузкам, поэтому
. По закону Гука деформации пропорциональны нагрузкам, поэтому
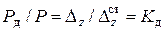 (6)
(6)
По закону Гука и напряжения пропорциональны нагрузкам
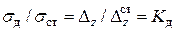 (9.5)
(9.5)
Здесь 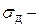 динамические напряжения, т.е. возникают в брусе при ударе;
динамические напряжения, т.е. возникают в брусе при ударе; 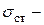 статические напряжения, возникают при статическом нагружении силой
статические напряжения, возникают при статическом нагружении силой 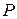 .
.
Из (9.4) и (9.5) следует
 (9.6)
(9.6)
Итак, деформации и напряжения в любом сечении бруса при ударе можно определить по (9.6), если вычислить 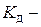 динамический коэффициент. А деформации
динамический коэффициент. А деформации 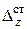 и напряжения
и напряжения 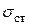 при любом виде статической нагрузки (осевой, изгибной, кручении и т.д.) мы умеем определять из вышеприведенных разделов.
при любом виде статической нагрузки (осевой, изгибной, кручении и т.д.) мы умеем определять из вышеприведенных разделов.
Для решения задачи используем закон сохранения энергии. Груз 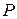 при падении проходит путь
при падении проходит путь 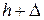 и совершает работу
и совершает работу 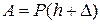 .
.
При статическом нагружении силой 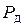 получим ту же деформацию, что и при ударе, потенциальная энергия деформации бруса при этом, как известно, определяется так
получим ту же деформацию, что и при ударе, потенциальная энергия деформации бруса при этом, как известно, определяется так 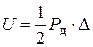 . Сила
. Сила 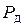 прикладывается в т. К, куда падает груз
прикладывается в т. К, куда падает груз 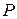 . По закону сохранения энергии
. По закону сохранения энергии 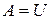 , т.е.
, т.е.
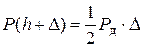 (7)
(7)
Из (6) 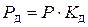 , подставим в (7) получим
, подставим в (7) получим
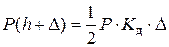 (8)
(8)
Сокращаем на 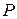 и учитывая из (9.4), что
и учитывая из (9.4), что 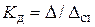 найдем
найдем
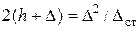 или
или 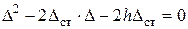 (9)
(9)
Относительно неизвестной 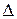 получили стандартное квадратное уравнение типа
получили стандартное квадратное уравнение типа 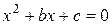
Здесь 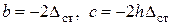 . Решение квадратного уравнения известно из справочников:
. Решение квадратного уравнения известно из справочников: 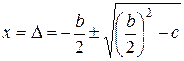 . В нашем случае получим
. В нашем случае получим
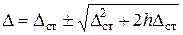 (10)
(10)
При ударе всегда 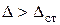 , поэтому выбираем знак (+) и формулу (10) преобразуем так
, поэтому выбираем знак (+) и формулу (10) преобразуем так
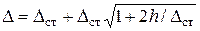 или окончательно
или окончательно 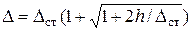 (11)
(11)
Согласно (9.4) 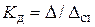 , тогда из (11) получим
, тогда из (11) получим
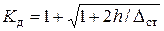 (9.8)
(9.8)
Величина Dст - статическая деформация бруса в точке удара от статического приложения силы 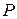 в точке «K» падения груза весом
в точке «K» падения груза весом 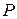 . Определяется известными методами:
. Определяется известными методами:
Рис. 9.1а: По закону Гука при осевой нагрузке
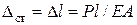
Рис. 9.1б: 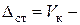 прогиб балки в т. K от силы
прогиб балки в т. K от силы 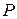 , приложенной в т. K. Определяется известным методом Клебша из раздела «Плоский изгиб балок».
, приложенной в т. K. Определяется известным методом Клебша из раздела «Плоский изгиб балок».
Скорость груза, падающего с высоты 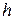 , как известно, определяется так
, как известно, определяется так 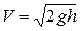 , откуда
, откуда 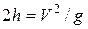 . Подставим это в (9.8) получим
. Подставим это в (9.8) получим
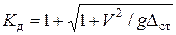 (9.9)
(9.9)
Преобразуем 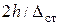 так:
так:
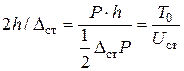 (12)
(12)
Здесь: 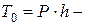 энергия падающего груза в момент начала удара;
энергия падающего груза в момент начала удара;
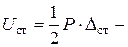 потенциальная энергия деформации бруса от статического нагружения его силой
потенциальная энергия деформации бруса от статического нагружения его силой 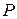 в т. K.
в т. K.
С учетом (12) из (9.8) найдем
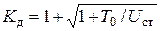 (9.10)
(9.10)
Из (9.8) следует, что чем больше 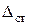 , т.е. чем больше деформируется брус от статической нагрузки
, т.е. чем больше деформируется брус от статической нагрузки 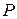 , тем меньше
, тем меньше 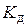 и по (9.6) меньше напряжения при ударе. Так появилась идея ставить в конструкциях, испытывающих ударные нагрузки, различные амортизаторы, рессоры, пружины и поясняется поговорка «знал бы, где упаду, подстелил бы солому».
и по (9.6) меньше напряжения при ударе. Так появилась идея ставить в конструкциях, испытывающих ударные нагрузки, различные амортизаторы, рессоры, пружины и поясняется поговорка «знал бы, где упаду, подстелил бы солому».
Пример. Порядок расчета балки на удар.
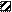  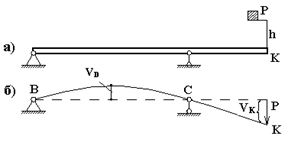 | На балку с высоты 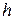 в т. K падает груз в т. K падает груз 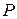 . Найти . Найти 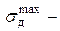 максимальное напряжение в балке от удара, максимальные прогибы в пролете и консоли. В т. K балки статически при- максимальное напряжение в балке от удара, максимальные прогибы в пролете и консоли. В т. K балки статически при- |
кладываем силу 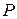 , равную весу груза (рис.б). Определяем от нее опорные реакции и строим эпюру
, равную весу груза (рис.б). Определяем от нее опорные реакции и строим эпюру 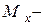 изгибающих моментов. Из Эп.
изгибающих моментов. Из Эп. 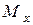 находим
находим 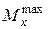 и, зная размеры и форму поперечного сечения балки, вычисляем
и, зная размеры и форму поперечного сечения балки, вычисляем 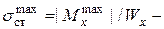 максимальные напряжения от статического нагружения. Для вычислений по (9.6) надо знать
максимальные напряжения от статического нагружения. Для вычислений по (9.6) надо знать 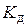 .
.
Для балки б) со статической силой 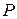 для двух участков запишем дифференциальные уравнения изгиба
для двух участков запишем дифференциальные уравнения изгиба 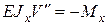 по методу Клебша, интегрируем их и из условий закрепления балки находим константы интегрирования. Строим график прогибов балки, приблизительный вид которого показан на рис.б. Находим
по методу Клебша, интегрируем их и из условий закрепления балки находим константы интегрирования. Строим график прогибов балки, приблизительный вид которого показан на рис.б. Находим 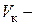 прогиб балки в сечении «K», это и есть
прогиб балки в сечении «K», это и есть 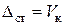 . По (9.8) вычисляем
. По (9.8) вычисляем 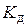 и далее
и далее
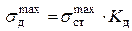
В консоли максимальный прогиб при ударе 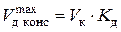 .
.
В пролете находим 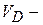 максимальный прогиб от статического нагружения и далее максимальный прогиб при ударе
максимальный прогиб от статического нагружения и далее максимальный прогиб при ударе 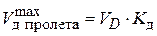 .
.
Дальше можно проверить балку на прочность и жесткость обычными методами.
Существует термин «падение с высоты 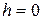 ». Из (9.8) в этом случае получим
». Из (9.8) в этом случае получим 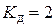 . Чтобы этого не было, груз надо опускать плавно не только до соприкосновения с конструкцией, но и дальше, при перемещении груза вместе с деформируемой конструкцией до полной их остановки.
. Чтобы этого не было, груз надо опускать плавно не только до соприкосновения с конструкцией, но и дальше, при перемещении груза вместе с деформируемой конструкцией до полной их остановки.
Литература
1. Сопротивление материалов. Под редакцией А.Ф. Смирнова. Учебник для вузов. М.: Высшая школа, 1975.- 480с.
2. Каюмов Р.А. Сопротивление материалов. Конспект лекций. Офсет, КГАСУ, Казань, 2010, 170с.
3. Мартышев В.П. Сопротивление материалов. Курс лекций. Под грифом УМО вузов РФ. КГАСУ ЗАО “Новое время”, 2010.- 200с.
4. Атаров Н.М. Сопротивление материалов в примерах и задачах, М.:Инфра-М, 2010. – 412с.
5. Уманский А.А. и др. Сборник задач по сопротивлению материалов. М.: Наука, 1973.- 336с.
 2015-01-30
2015-01-30 1204
1204







