2015-01-30
1654
Выведем формулы для определения нормальных напряжений в брусьях большой кривизны.
При выводе этих формул предполагается, что:
1) кривой брус является плоским (т.е. ось его представляет собой плоскую кривую);
2) брус симметричен относительно плоскости, в которой расположена его ось, а внешние силы действуют в этой плоскости;
3) поперечные сечения бруса, плоские до его деформации, остаются плоскими и после деформации (гипотеза плоских сечений);
4) давление продольных волокон бруса друг на друга не влияет существенно на распределение напряжений в брусе, а потому его можно не учитывать.
При изгибе брусьев малой кривизны нормальные напряжения с достаточной степенью точности можно определять по формуле Навье для балок с прямой осью. Максимальные напряжения, подсчитанные по формуле Навье для бруса прямоугольного сечения с отношением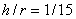 
, отличаются на 2% от напряжений, вычисленных по формулам для бруса большой кривизны; при 
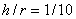- на 3,5%, при 
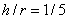- на 7%.
Рассмотрим случай чистого изгиба бруса большой кривизны (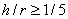
) (рис.5). Предполагаем, что радиус 
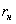нейтрального слоя неизвестен и не совпадает с радиусом R оси стержня.
|
|
|
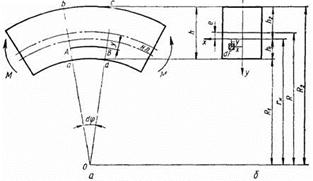
Рис.5
При выводе формулы для определения нормальных напряжений в брусе большой кривизны исходят из тех же гипотез, что и при выводе формулы Навье, т. е пользуются гипотезой плоских сечений и гипотезой о том, что продольные волокна материала не давят одно на другое. Выбираем направление осей сечения х и у, как показано на рис.6 (при этом ось х считается совпадающей с нейтральной линией, положение которой пока неизвестно). Направление у к центру кривизны принято за положительное.
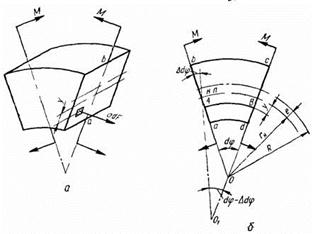
Рис.6
Рассмотрим статическую сторону задачи и запишем условие равновесия применительно к элементу бруса (рис. 6, а), оставшемся после удаления отсеченных частей. Для нашего случая, когда в сечении действует один силовой фактор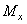 
, будем иметь
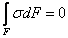; (4)
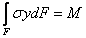. (5)
В силу симметрии F
.
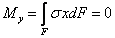Рассмотрим геометрическую сторону задачи. Относительное удлинение произвольно выделенного элементарного участка АВ, находящегося на расстоянии у от нейтральной линии (рис. 6, б) и получившего в результате деформации удлинение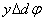 
, равно
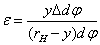, (6)
где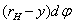 
– длина элемента до деформации.
Из рассмотрения физической стороны задачи, определяемой законом Гука
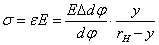, (7)
условие (4) перепишем в виде
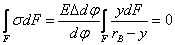
Так как
,
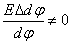то
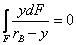. (8)
Из (5) находим
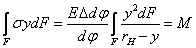(9)
Так как
,
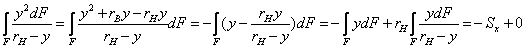или
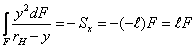, (10)
Можем представить (9) так:
.
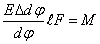Отсюда
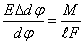, (11)
где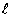 
— расстояние от нейтральной линии до центра тяжести (эксцентриситет); F - площадь поперечного сечения.
Подставив (11) в (7), найдем формулу для определения нормальных напряжений при изгибе
|
|
|
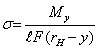, (12)
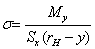. (13)
Здесь М — изгибающий момент в сечении; S x — статический момент площади сечения кривого бруса относительно нейтральной линии.
Из анализа (12) или (13) видно, что нормальные напряжения по высоте распределяются по гиперболическому закону (рис. 7, б).
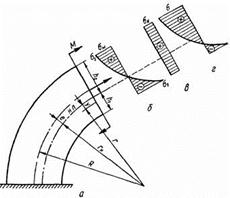
Рис. 7
Абсолютные величины напряжений в крайних волокнах сечения бруса согласно (12) определяются по формулам
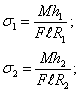(14)
где R 1 и R 2 — соответственно радиусы кривизны внутренних и внешних волокон кривого бруса; h 1 и h 2 — расстояния от нейтральной линии до этих волокон. Знак напряжения определяется по направлению изгибающего момента в сечении.
Формулы (12) - (14) могут быть использованы, если известна входящая в эти формулы величина 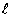или радиус нейтрального слоя 
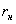поскольку
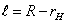, (15)
где R — радиус слоя, в котором расположены центры тяжести сечения бруса. Радиус 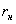определим из уравнения (8).
Произведя замену переменных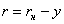 
или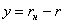 
, перепишем уравнение (8) в следующем виде:
.
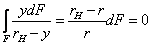или
.
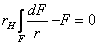Отсюда
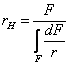. (16)
Так как для прямоугольного сечения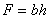 
(h - высота сечения; b - ширина сечения); 
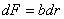, формула (16) может быть описана в виде
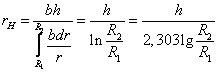(17)
Воспользовавшись рядом
,
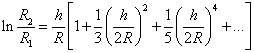получим
.
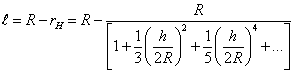В первом приближении
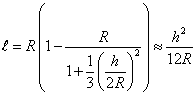. (18)
Во втором приближении
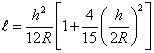. (19)
На основании (16) аналогичным путем можно получить приближение для 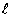в случае других форм поперечного сечения. Из (15) по известным 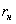могут быть определены величины .
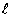- Понятия об устойчивых и неустойчивых формах равновесия систем. Устойчивость сжатых стержней и критическая сила.
В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых один или два размера поперечного сечения малы по сравнению с длиной стержня. Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней. Опыт показывает, что при достижении сжимающей силой F некоторой критической величины, равной F кр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении F кр стержень начинает интенсивно искривляться (выпучиваться). При этом новым (моментным) равновесным состоянием упругого длинного стержня (при F > F кр) становится некоторая новая уже криволинейная форма. Это явление носит название потери устойчивости.
