Путем объединения элементарных трехмерных преобразований можно получить другие преобразования. В этом разделе показано, как это сделать. Задача состоит в том, чтобы преобразовать отрезки P1P2 и P1P3 (рис. 2.5) из начальной позиции в конечную. Точка Pi переносится в начало координат, P1P2 располагается вдоль отрицательной полуоси x, а P1P3 помещается в плоскости yz в той ее половине, где ось у положительна. На длины отрезков преобразование не воздействует.
Как и прежде, разобьем сложную задачу на более простые. В данном случае преобразование можно выполнить за четыре шага:
1. Перенос точки Pi в начало координат.
2. Поворот вокруг оси у до совмещения P1P2 с плоскостью уz.
3. Поворот вокруг оси x до совмещения P1P2 с отрицательной полуосью Z.
4. Поворот вокруг оси z до совмещения P1P3 с плоскостью yz.
Шаг 1. Перенос Ρ1 в начало координат:
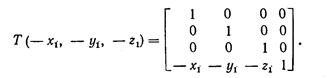
Применение Τ к P1, Р2 и Р3 дает
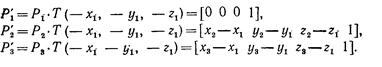
Шаг 2. Поворот вокруг оси у. На рис. 2.5 показаны отрезки P1P2 после шага 1 и проекция P1P2 на плоскость xz. Поворот производится на положительный угол θ, для которого
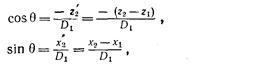
где 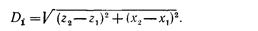
Тогда
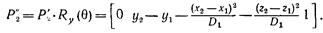
Как и ожидалось, x -компонента Р2 равна нулю.
Шаг 3. Поворот вокруг оси х. На рис. 2.6 показан отрезок P1P2
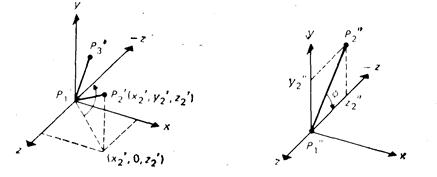
Рис. 2.5. Композиция преобразований
после шага 2. Поворот производится на отрицательный угол φ, для которого 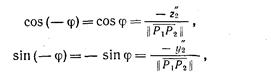
где 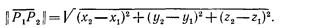
Запись 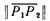 обозначает длину
обозначает длину 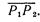 Результатом поворота на шаге 3 является
Результатом поворота на шаге 3 является
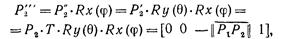
т. е. 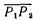 теперь совпадает с отрицательной полуосью z.
теперь совпадает с отрицательной полуосью z.
Шаг 4. Поворот вокруг оси z. На рис. 2.6 показаны 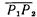 и
и 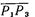 после шага 3, когда Р2'" лежит на отрицательной полуоси z, а Р3'" - в точке
после шага 3, когда Р2'" лежит на отрицательной полуоси z, а Р3'" - в точке
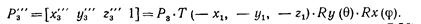
Поворот производится на
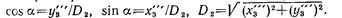
положительный угол a, для которого Шаг 4 является последним шагом, после которого получается конечный результат, показанный на рис. 2.6. Результирующая матрица
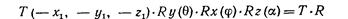
описывает искомое преобразование, где 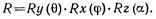
Рис. 2.6. Окончание композиции преобразований
 2015-01-30
2015-01-30 963
963








