Аффинные преобразования на плоскости

Это частный случай преобразований, который достаточно часто используется при создании графических пакетов.

Зададим некоторую двумерную систему координат (x,у). Аффинное преобразование на плоскости описывается формулами

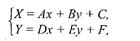
где А, В,..., F — константы. Значение (X, Y) можно рассматривать как координаты в новой системе координат.

Обратное преобразование (X, Y) в (х, у) также является аффинным:

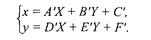
Аффинное преобразование удобно записывать в матричном виде. Константы А, В..... F образуют матрицу преобразования, которая, будучи умноженной на матрицу-столбец координат (x, у), дает матрицу-столбец (X, Y). Однако, чтобы учесть константы С и F, необходимо перейти к так называемым однородным координатам — прибавим еще одну строку в матрицах координат:

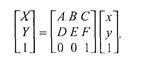
Теперь рассмотрим частные случаи аффинного преобразования.

1. Параллельный сдвиг координат (рис. 2. 9).

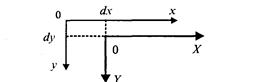
Рис. 2.9. Параллельный сдвиг координат

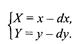
В матричной форме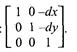

Обратное преобразование: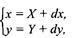

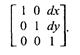
2. Растяжение-сжатие осей координат (рис. 2. 10).

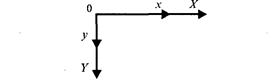
Рис. 2.10. Растяжение-сжатие осей координат

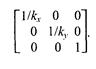
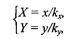
Обратное преобразование: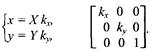

Коэффициенты k_x и k_y могут быть отрицательными. Например, k_x = -1 соответствует зеркальному отражению относительно оси y.

3. Поворот (рис. 2. 11).

Рис.2.11. Поворот

Обратное преобразование соответствует повороту системы (X, Y) на угол (-α).

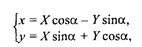
Свойства аффинного преобразования.

• Любое аффинное преобразование может быть представлено как последовательность операций из числа указанных простейших: сдвиг, растяжение/сжатие и поворот.

• Сохраняются прямизна линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и соотношение площадей фигур.