2015-01-30
605
| s0 =400, h =80 | ||||
| x | f1 (x) | f2 (x) | f3 (x) | f4 (x) |
Необходимо определить, какой объем ресурсов нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей.
Представим процесс распределения ресурсов между хозяйствующими субъектами как n -шаговый процесс управления (номер шага совпадает с условным номером хозяйствующего субъекта). Пусть sk (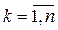
) – параметр состояния, т.е. количество свободных средств после k -го шага для распределения между оставшимися (n – k) хозяйствующими субъектами. Тогда уравнения состояний можно записать в следующем виде:
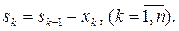(7.1)
Введем в рассмотрение функцию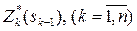 
– условно оптимальная совокупная прибыль, полученная от k -го, (k +1)-го, …, n -го хозяйствующих субъектов, если между ними оптимальным образом распределялись ресурсы в объеме sk-1 (
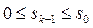). Множество возможных управленческих решений относительно размера распределяемых ресурсов на k -ом шаге можно представить следующим образом: 
.
|
|
|
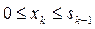Тогда рекуррентные уравнения Р.Э. Беллмана (обратная схема) будут иметь вид:
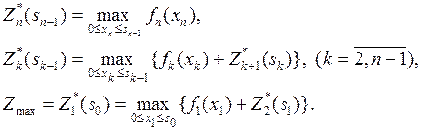(7.2)
Далее по полученным результатам условной оптимизации можно определить оптимальное распределение ресурсов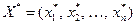 
по следующей схеме:
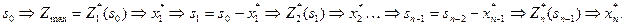
Фрагмент MathCAD-документа, реализующий решение данной задачи, приведен в приложении 4. На рис. 58 представлен блок ввода исходных данных. Вектор Q представляет множество возможных управленческих решений xi, матрица F определяет прибыльность предприятий в зависимости от выделенных ресурсов (размерности Q и F можно изменять). Особенностью программы является то, что первые компоненты вектора Q и матрицы F должны быть нулевыми, несоблюдение данного условия приведет к ошибочным результатам.
Рис. 58. Фрагмент MathCAD-документа: система исходных данных задачи распределения ресурсов
На рис. 59 представлены результаты решения, в соответствии с которыми оптимальным распределением является: выделение 240 усл. ед. третьему хозяйствующему субъекту и 160 усл. ед. – четвертому. Данное распределение обеспечит максимум прибыли в размере 203 усл. ед.
Рис. 59. Фрагмент MathCAD-документа: результаты решения задачи распределения ресурсов
