Уравнение для численности населения

Уравнение (1) основано на простейшей гипотезе, используемой обычно в теории популяций: скорость изменения численности популяции пропорциональна самой численности. Коэффициент прироста населения n(y, z) представляет собой разность между коэффициентом рождаемости b(y, z) и коэффициентом смертности населения d(y, z)

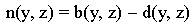(15)

Коэффициенты рождаемости и смертности, а следовательно, и коэффициент прироста населения зависят от количества продукции на человека и от уровня природного капитала. Запас природного капитала может быть представлен как состояние тех компонентов окружающей среды, которые влияют на состояние здоровья человека и дают ему возможность жить полноценной жизнью. К ним можно отнести, например, воду и воздух. Для количественного выражения природного капитала вводится фиктивная переменная z, меняющаяся от 0 до1. Если окружающая среда совсем не загрязнена, то считается, что z =1. Значение z=0 выражает другой предельный случай, когда окружающая среда настолько загрязнена, что представляет собой наибольшую опасность человеческому здоровью и экономике. Согласно принятым для коэффициентов рождаемости и смертности зависимостями от переменных y и z

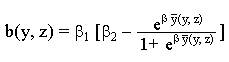(16)

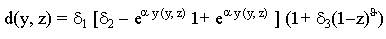(17)

Коэффициенты b(y,z) и d(y,z) уменьшаются с увеличением количества чистой продукции на человека 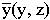. Кроме того, коэффициент смертности растет с уменьшением природного капитала. Чистая продукция на душу населения определяется как продукция на человека за вычетом расходов на управление за уровнем загрязнений, выражаемых функцией с(у, z),

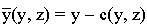(18)

Расходы на управление уровнем загрязнений с(y,z) зависят, в свою очередь, от уровня экономики и состояния окружающей среды

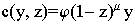(19)

Расходы на управление увеличиваются линейно сростом экономики y и уменьшается по мере улучшения качества среды, т.е. роста переменной z.

При постоянном коэффициенте прироста n(y, z) = n₀ = const уравнение (11) представляет собой классическую экспоненциальную модель для численности одиночной популяции. В том случае решение (11) запишется в аналитическом виде

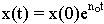(20)

Экспоненциальная модель (20) при n₀ > 0 предсказывает неограниченный рост, при n₀ = 0 – постоянную численность популяции, а при n₀ < 0 – падение численности.