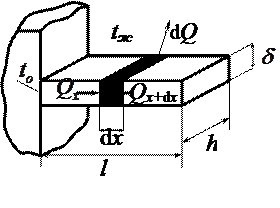 Постановка задачи. Рассмотрим ребро постоянного поперечного сечения f = const, периметр сечения u = const. Длина ребра l. Коэффициент теплопроводности материала
Постановка задачи. Рассмотрим ребро постоянного поперечного сечения f = const, периметр сечения u = const. Длина ребра l. Коэффициент теплопроводности материала
l = const.
У основания ребра поддерживается температура 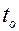 . Ребро находится в среде с температурой
. Ребро находится в среде с температурой  , коэффициент теплоотдачи a. Принимая, что f мало (ребро тонкое), а l достаточно велико, пренебрегаем градиентом температуры в поперечном направлении сечения ребра (температура центра сечения ребра
, коэффициент теплоотдачи a. Принимая, что f мало (ребро тонкое), а l достаточно велико, пренебрегаем градиентом температуры в поперечном направлении сечения ребра (температура центра сечения ребра 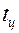 и температура его поверхности
и температура его поверхности 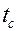 равны). Записывая равенство
равны). Записывая равенство 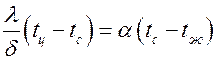 , получаем
, получаем 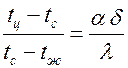 → 0. Если подставить размерность величин, стоящих в правой части равенства, то размерности сократятся. Безразмерный комплекс величин
→ 0. Если подставить размерность величин, стоящих в правой части равенства, то размерности сократятся. Безразмерный комплекс величин 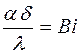 называется безразмерным числом Био. Ребро считается тонким, если
называется безразмерным числом Био. Ребро считается тонким, если 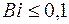 .
.
Полагая, что температура изменяется только вдоль ребра, найдем закономерность изменения температуры по длине ребра и тепловой поток, передаваемый с поверхности ребра в окружающую среду.
Для решения задачи выделим на расстоянии х от основания ребра элемент длиной d x и составим для него уравнение теплового баланса
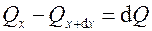 .
.
Здесь 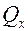 и
и 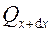 – тепловые потоки, передающиеся теплопроводностью согласно закону Био-Фурье. Их можно представить в виде
– тепловые потоки, передающиеся теплопроводностью согласно закону Био-Фурье. Их можно представить в виде 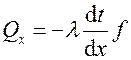 ,
, 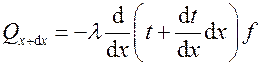 ,
, 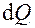 – теплота, отдаваемая с поверхности выделенного элемента ребра,
– теплота, отдаваемая с поверхности выделенного элемента ребра, 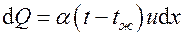 .
.
Введем понятие избыточной температуры 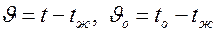 . Подставим значения
. Подставим значения 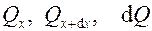 .
.
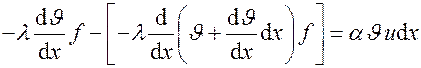 .
.
Раскрывая скобки и сокращая на d x левую и правую части, получаем
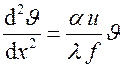 или
или 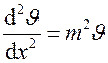 ,
,
где 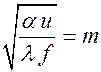 . Общее решение уравнения имеет вид
. Общее решение уравнения имеет вид
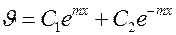 .
.
Значения постоянных интегрирования С 1 и С 2 найдем из граничных условий: при x = 0 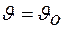 ; при x = l
; при x = l 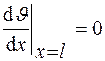 , т.е. количеством теплоты, переданным в окружающую среду с торца ребра, пренебрегаем, так как ребро тонкое. Подставляя граничные условия в общее решение, находим
, т.е. количеством теплоты, переданным в окружающую среду с торца ребра, пренебрегаем, так как ребро тонкое. Подставляя граничные условия в общее решение, находим 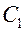 и
и 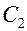 и получаем частное решение в виде
и получаем частное решение в виде
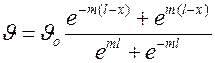 .
.
Из математики известно, что 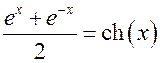 , а
, а 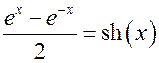 . Умножим числитель и знаменатель на 1/2.
. Умножим числитель и знаменатель на 1/2.
Тогда 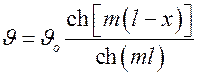 .
.
Следовательно, температура по длине ребра изменяется по экспоненциальному закону.
Тепловой поток, передаваемый ребром в окружающую среду, и равный тепловому потоку, прошедшему теплопроводностью через основание ребра, найдется по формуле

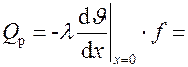
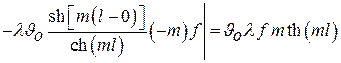 .
.
Подставляя значение m, получаем
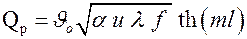 .
.
Теплопередача через ребристую стенку (уточненный расчет)
Введем понятие коэффициента эффективности работы ребра 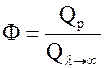 , где
, где 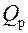 – тепловой поток, передаваемый ребром в окружающую среду;
– тепловой поток, передаваемый ребром в окружающую среду; 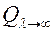 – тепловой поток, передаваемый этим ребром, когда температура вдоль него не изменяется, что теоретически возможно при l = ¥, поэтому
– тепловой поток, передаваемый этим ребром, когда температура вдоль него не изменяется, что теоретически возможно при l = ¥, поэтому 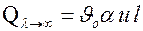 . Тогда
. Тогда
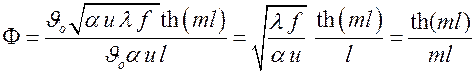 .
.
С введением коэффициента Ф выражение для теплового потока с поверхности ребра запишется следующим образом 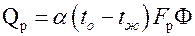 .
.
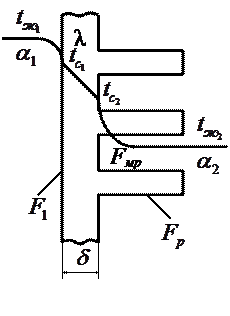 Рассмотрим плоскую стенку с прямыми ребрами (рис. 1.14). Условия задачи и схема ее решения аналогичны приведенным выше при приближенном расчете задачи.
Рассмотрим плоскую стенку с прямыми ребрами (рис. 1.14). Условия задачи и схема ее решения аналогичны приведенным выше при приближенном расчете задачи.
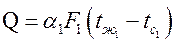 .
.
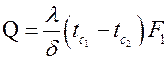 .
.
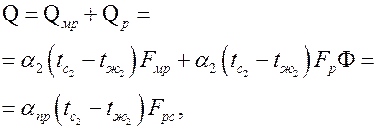 где
где 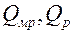 – тепловые потоки с межреберной поверхности и поверхности ребер ребристой стенки;
– тепловые потоки с межреберной поверхности и поверхности ребер ребристой стенки; 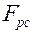 – поверхность ребристой стенки,
– поверхность ребристой стенки, 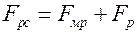 ;
; 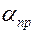 – приведенный коэффициент теплоотдачи,
– приведенный коэффициент теплоотдачи, 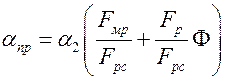 .
.
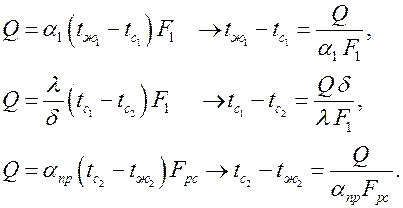
Выражая разность температур из каждого уравнения, и складывая их,
получаем
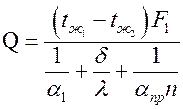 .
.
Если известна температура 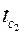 , то рассчитать теплоотдачу с ребристой поверхности можно проще, не прибегая к вычислению приведенного коэффициента теплоотдачи.
, то рассчитать теплоотдачу с ребристой поверхности можно проще, не прибегая к вычислению приведенного коэффициента теплоотдачи.
В этом случае тепловой поток, передаваемый с ребристой поверхности, определится по формуле
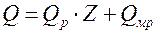 ,
,
где 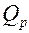 – тепловой поток с поверхности одного ребра,
– тепловой поток с поверхности одного ребра, 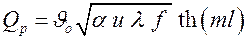 ; Z – количество ребер;
; Z – количество ребер; 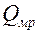 – тепловой поток с межреберной поверхности.
– тепловой поток с межреберной поверхности.
При расчете считаем, что коэффициент теплоотдачи с поверхности ребер и межреберного пространства одинаковый.
Лекция 6. Раздел 4. Теплопроводность при нестационарном режиме
 2014-04-09
2014-04-09 5682
5682








