Для многослойной цилиндрической стенки линейная плотность теплового потока будет находиться по такой же схеме, как и для однослойной, за исключением того, что тепловой поток теплопроводностью пройдет не через один, а через n слоев стенки. Формула для расчета 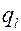 для n -слойной цилиндрической стенки будет иметь вид
для n -слойной цилиндрической стенки будет иметь вид
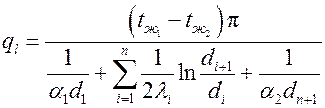 ,
, 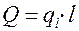 .
.
Теплопроводность тел неправильной формы
На практике могут встречаться тела с неправильными геометрическими формами (например, стенки, у которых F 1 и F 2 различны).
Определить тепловой поток, передаваемый теплопроводностью как геометрически правильных стенок, т.е. плоской, цилиндрической и шаровой, так и близких к ним стенок неправильных геометрических форм можно по следующей формуле [4]:
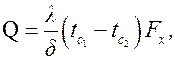
где d – средняя толщина стенки, 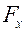 – зависит от формы стенки. Так, для плоской или цилиндрической стенки с площадью внутренней поверхности F 1 и внешней F 2 при
– зависит от формы стенки. Так, для плоской или цилиндрической стенки с площадью внутренней поверхности F 1 и внешней F 2 при 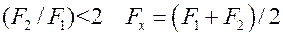 . Для цилиндрической стенки при
. Для цилиндрической стенки при 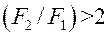
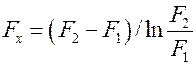 . Для шаровой стенки
. Для шаровой стенки 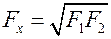 .
.
Для расчета теплопередачи через цилиндрическую стенку вместо точной формулы можно пользоваться приближенной
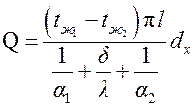 ,
,
где 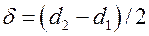 , a
, a 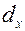 – некоторый расчетный диаметр, который выбирается из следующих соображений:
– некоторый расчетный диаметр, который выбирается из следующих соображений:
если 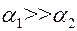 , то
, то 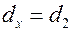 ; если
; если 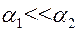 , то
, то 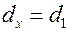 ;
;
если 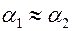 , то
, то 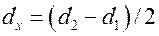 .
.
 Критический диаметр тепловой изоляции
Критический диаметр тепловой изоляции
Назначение тепловой изоляции – уменьшать потери теплоты в окружающую среду. Рассмотрим трубопровод, по которому течет жидкость с температурой 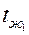 = const, а снаружи трубы находится жидкость с температурой
= const, а снаружи трубы находится жидкость с температурой  = const. Причем
= const. Причем 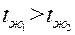 . Коэффициенты теплоотдачи
. Коэффициенты теплоотдачи 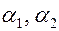 заданы.
заданы.
Для уменьшения тепловых потерь нанесем слой тепловой изоляции на внешнюю поверхность трубы. Выясним, как влияет толщина (диаметр) тепловой изоляции на величину тепловых потерь 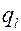 . Плотность теплового потока, передаваемая в процессе теплопередачи через двухслойную цилиндрическую стенку, определится по формуле
. Плотность теплового потока, передаваемая в процессе теплопередачи через двухслойную цилиндрическую стенку, определится по формуле
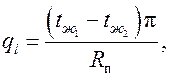
где 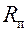 – полное термическое сопротивление двухслойной цилиндрической стенки,
– полное термическое сопротивление двухслойной цилиндрической стенки, 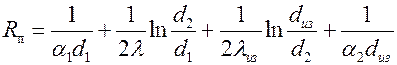 . Обозначим
. Обозначим
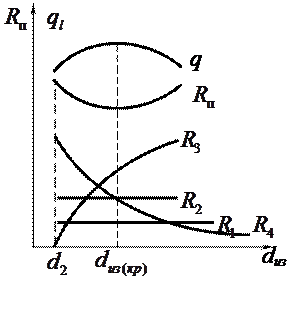 слагаемые, стоящие в правой части
слагаемые, стоящие в правой части 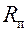 ,
, 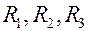 ,
,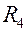 . Тогда
. Тогда 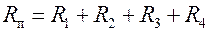 . Величины
. Величины 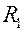 и
и 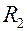 не зависят от толщины изоляции (
не зависят от толщины изоляции (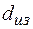 ), а
), а 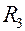 и
и 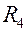 – зависят, причем при увеличении
– зависят, причем при увеличении 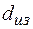 величина
величина 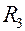 увеличивается, а
увеличивается, а 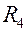 – уменьшается.
– уменьшается.
Полное термическое сопротивление 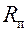 , определяемое характером изменения составляющих
, определяемое характером изменения составляющих 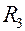 и
и 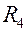 , имеет минимум. Значение диаметра изоляции, соответствующее минимальному термическому сопротивлению теплопередачи, называется критическим диаметром изоляции и обозначается
, имеет минимум. Значение диаметра изоляции, соответствующее минимальному термическому сопротивлению теплопередачи, называется критическим диаметром изоляции и обозначается 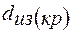 . Для определения его значения возьмем производную от
. Для определения его значения возьмем производную от 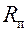 по
по 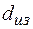 и приравняем ее нулю:
и приравняем ее нулю:
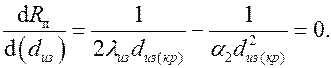
Отсюда
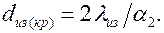
Следовательно, при 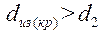 с увеличением толщины изоляции
с увеличением толщины изоляции 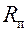 уменьшается, а
уменьшается, а 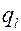 согласно (1.42) возрастает. При
согласно (1.42) возрастает. При 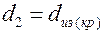
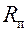 будет минимальное, а линейная плотность теплового потока
будет минимальное, а линейная плотность теплового потока 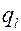 – максимальная. И только при
– максимальная. И только при 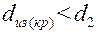 тепловые потери будут уменьшаться.
тепловые потери будут уменьшаться.
Поэтому, выбрав какой-либо теплоизоляционный материал для покрытия цилиндрической поверхности, прежде всего нужно рассчитать критический диаметр тепловой изоляции. Если окажется, что 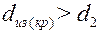 , то применение выбранного теплоизоляционного материала в качестве тепловой изоляции нецелесообразно.
, то применение выбранного теплоизоляционного материала в качестве тепловой изоляции нецелесообразно.
Лекция 4,5. Раздел 3. Интенсификация процесса теплопередачи
 2014-04-09
2014-04-09 1523
1523








