Плоскости в трёхмерном пространстве

Уточним, прежде всего, понятие «плоскость» с помощью определения, хорошо согласованного с нашими интуитивными представлениями.

`N M0 M

Пусть` 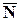– некоторый ненулевой вектор, M₀(x₀, y₀, z₀) –точка. Плоскостью Р называется множество точек M таких, что векторы 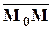и перпендикулярны:

P = { M | 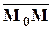перпендикулярен }.

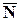Таким образом, чтобы задать плоскость нужна точка M₀ , через которую эта плоскость проходит, и вектор 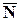, перпендикулярный к плоскости – он называется вектором нормали.

Теорема 1. Плоскости и только они являются поверхностями 1 –го порядка в трёхмерном пространстве.

Доказательство. Пусть P –плоскость, M₀(x₀, y₀, z₀) –точка плоскости,

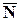= (A, B, C) –вектор нормали. Запишем условия того, что некоторая (текущая) точка M(x, y, z) лежит на плоскости:

.

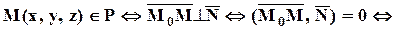
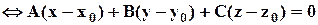Последнее соотношение (полученное как результат вычисления скалярного произведения в координатной форме) есть уравнение плоскости. Ясно, что это – уравнение первой степени.

Обратно, рассмотрим произвольное уравнение 1 –й степени:

Ax + By + Cz + D = 0.

Здесь хотя бы одно из чисел A, B, C не равно 0. Возьмем произвольную точку M₀(x₀, y₀, z₀), координаты которой удовлетворяют данному уравнению:

Ax₀ + By₀ + Cz₀ + D = 0.

Вычтем это равенство из общего уравнения:

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

Получили уравнение, равносильное исходному. Но из первой части доказательства видно, что это уравнение задает плоскость, проходящую через M₀(x₀, y₀, z₀) перпендикулярно вектору 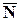= (A, B, C). Итак, уравнение Ax + By + Cz + D = 0 задает плоскость. Теорема доказана.

Замечание. Подчеркнём важную роль, которую играет вектор нормали при работе с плоскостью. Если дано уравнение, значит вектор нормали известен. Обратно, если известен вектор нормали, то, зная хотя бы одну точку плоскости, можно написать её уравнение.

Рассмотрим некоторые частные случаи уравнения плоскости. Если D = 0, то точка O(0, 0, 0) удовлетворяет уравнению. Значит плоскость Ax + By + Cz = 0 проходит через начало координат.

Если A = B = 0, т.е. уравнение имеет вид Cz + D = 0, или 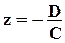, то вектор нормали коллинеарен вектору `k = (0, 0, 1). Поэтому плоскость перпендикулярна оси OZ, а значит параллельна плоскости XOY. Координатная плоскость XOY имеет уравнение z = 0.

Аналогично, x = 0 – уравнение координатной плоскости YOZ; x = a – уравнение плоскости, параллельной YOZ; y = 0 – уравнение плоскости XOZ; y = b – уравнение плоскости, параллельной XOZ.

Если равна нулю только одна из координат вектора нормали, то нормаль перпендикулярна, а плоскость, следовательно, параллельна соответствующей оси. Например, плоскость Ax + Cz + D = 0 параллельна оси OY (возможно, содержит эту ось).

Вопросы о взаимном расположении плоскостей решаются с помощью вектора нормали. Пусть две плоскости заданы своими уравнениями:

A₁x + B₁y + C₁z + D₁ = 0 ( плоскость Р₁),

A₂x + B₂y + C₂z + D₂ = 0 ( плоскость Р₂).

Запишем в краткой, символической форме условия параллельности и перпендикулярности плоскостей:

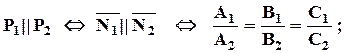
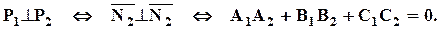
Угол между плоскостями равен углу между векторами нормали и находится с помощью скалярного произведения

Как известно, через любые 3 точки, не лежащие на одной прямой, можно провести единственную плоскость. Научимся решать эту важную задачу в общем виде, а затем рассмотрим пример. Пусть точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃) не лежат на одной прямой.

Мы помним, что главное для записи уравнения плоскости – найти вектор нормали, т.е. какой–нибудь вектор, перпендикулярный плоскости. В качестве такого вектора можно взять векторное произведение:

,

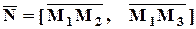так как векторное произведение, по определению, перпендикулярно каждому из сомножителей (см. раздел 4.3). Вычисляя координаты 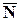, получим

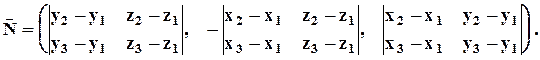
В качестве точки плоскости для записи уравнения можно взять любую из точек M₁, M₂, M₃. Возьмём, например, M₁ :

.

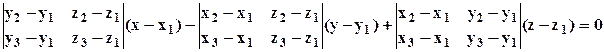Левую часть равенства можно записать как определитель 3 –го порядка. Получаем уравнение в виде:

.

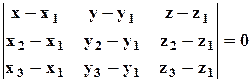Приведём другой способ вывода уравнения плоскости, проходящей через 3 данные точки. Пусть M(x, y, z) – произвольная (текущая) точка. Очевидно, M лежит на плоскости тогда и только тогда, когда векторы 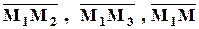компланарны.

Условие компланарности векторов записывается с помощью смешанного произведения (см. 4.4):

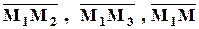( ) = 0.

Или, в координатной форме:

.

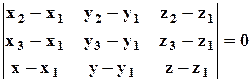Заметим, что получено то же самое уравнение, так как перестановка строк, как мы знаем, может лишь изменить знак определителя. Но если определитель равен 0, то он не меняется.

Решим еще одну задачу о плоскости. Найдём расстояние от точки

M₀(x₀, y₀, z₀) до плоскости Ax + By + Cz + D = 0.

Обозначим через M₁(x₁, y₁, z₁) –основание перпендикуляра, опущенного из M₀ на плоскость. Тогда вектор 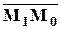, очевидно, коллинеарен вектору нормали 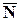= (A, B, C). Вычислим их скалярное произведение: 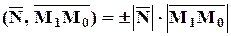(так как косинус угла равен ±1, в зависимости от совпадения или несовпадения направлений векторов). С другой стороны, в координатной форме:

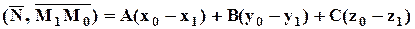.Так как точка M₁(x₁, y₁, z₁) лежит на плоскости, то Ax₁ + By₁ + Cz₁ + D = 0 и, раскрывая скобки, получаем:

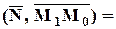Ax₀ + By₀ + Cz₀ + D.

Сравнивая два полученных выражения для 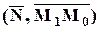, находим расстояние d от точки до плоскости:

.

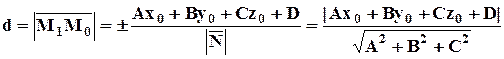Знак ±мы заменили абсолютной величиной, поскольку расстояние – величина всегда положительная.

ПРЕДЕЛ ФУНКЦИИ Предел функции в точке

Односторонние пределы

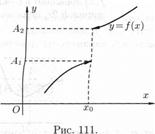
В определении предела функции lim f(x) = А считается, что х стремится к х₀ любым способом: оставаясь мень­шим, чем х₀ (слева от х₀), большим, чем х₀ (справа от х₀), или колеблясь около точки х_0. Бывают случаи, когда способ при­ближения аргумента х к х₀ существен­но влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.

Число А ₁ называется пределом функции у = f(x) слева в точке х₀, если для любого число ε > 0 существует число δ = δ(ε) > 0 такое, что при х € (х₀ —δ; х₀), выполняется неравенство |f(х) — A₁| < ε. Предел слева записывают так: lim f(x) = А₁ или коротко: f(хо — 0) = А₁ (см. рис. 111). х→х₀ -0

Аналогично определяется предел функции справа, запишем его с по­мощью символов:

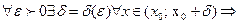( | f (х) - А₂\ < ε) 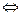lim f(x) = А₂

х→х₀₊0

Пределы функции слева и справа называются односторонними пре­делами. Очевидно, если существует lim f(x) = А, то существуют и оба односторонних предела, причем А=А₁= А₂.

Основные теоремы о пределах

Формулировка и доказательство теорем для случаев, когда х→х₀ и х→∞, аналогичны. В приводимых теоремах будем считать, что пределы lim f(x), lim (x) существуют.

Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

lim (f(x) ± (х)) = lim f(x) ± lim (x)

х→х₀ х→х₀ х→х₀

Следствие 1. Функция может иметь только один предел при х→х₀

Теорема 2. Предел произведения двух функций равен произведению их преде­лов:

lim (f(x)· (х)) = lim f(x)· lim (x)

х→х₀ х→х₀ х→х₀

Следствие 2. Постоянный множитель можно выносить за знак предела: lim с· f(x) = с·lim f(x). х→х₀ х→х₀

Следствие 3. Предел степени с натуральным показателем равен той же степени lim (f(x))ⁿ = (lim f(х))ⁿ.

х→х₀ х→х₀

В частности, lim xⁿ = xⁿ, n € N

х→х₀

Теорема 3 Предел дроби равен пределу числителя, деленному на предел зна­менателя, если предел знаменателя не равен нулю: =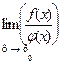

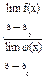
1 –Первый замечательный предел: Читается: предел от­ношения синуса к его аргументу равен единице, когда аргумент стремится к нулю

2 -Второй замечательный предел

Функция у = е^х называется экспоненциальной, употребляется также обозначение е ^х = ехр(x).