Пусть функция 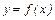 имеет в точке
имеет в точке 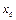 конечную, не равную нулю производную. Можно показать, что приращение функции в окрестности этой точки может быть представлено в виде суммы двух слагаемых
конечную, не равную нулю производную. Можно показать, что приращение функции в окрестности этой точки может быть представлено в виде суммы двух слагаемых 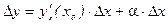 , где
, где 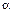 – бесконечно малая величина при
– бесконечно малая величина при 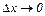 .Так как производная функции равна константе, то слагаемое
.Так как производная функции равна константе, то слагаемое 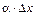 представляет собой бесконечно малую величину более высокого порядка малости по сравнению с
представляет собой бесконечно малую величину более высокого порядка малости по сравнению с 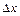 и с
и с 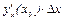 (так как является произведением двух бесконечно малых величин), а первое слагаемое будет являться главной частью приращения функции.
(так как является произведением двух бесконечно малых величин), а первое слагаемое будет являться главной частью приращения функции.
Дифференциалом функции 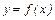 в точке
в точке 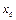 называется главная линейная относительно приращения аргумента
называется главная линейная относительно приращения аргумента 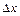 часть приращения функции
часть приращения функции 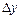 и обозначается
и обозначается 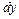 .
.
Формула вычисления дифференциала имеет вид 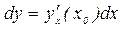
 2015-01-30
2015-01-30 373
373








