2015-01-30
1465
Пусть дана дифференцируемая функция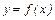 
и требуется составить уравнение касательной к графику этой функции в точке 
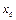. Из геометрического смысла производной следует, что значение производной в точке 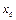равно угловому коэффициенту касательной, проведенной к графику функции в этой точке, т.е. 
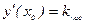, причем 
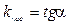, а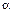 
– угол наклона касательной с положительным направлением оси OX.
Для составления уравнения касательной воспользуемся уравнением прямой, проходящей через точку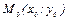 
с заданным угловым коэффициентом k: 
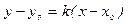, где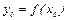 
, 
.
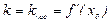Т.о. уравнение касательной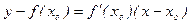 
или 
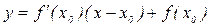. (3)
Нормалью к кривой в заданной точке называется прямая, проходящая через точку касания перпендикулярно касательной.
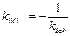Из геометрии известно, что угловые коэффициенты взаимно перпендикулярных прямых связаны соотношением:.
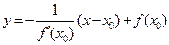
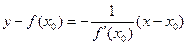
Поэтому уравнение нормали имеет вид: или
