2015-01-30
1062
Найдем опорные реакции. Балка имеет шарнирное опирание и для определения двух не равных нулю опорных реакций RA и RB (горизонтальная реакция HA = 0) составим два независимых уравнения статики. Рациональными уравнениями, в каждое из которых входит одна неизвестная реакция, в данном случае являются:
; 
,
; 
.
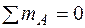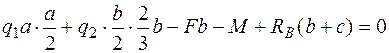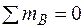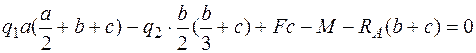Напомним как определяется момент от треугольной нагрузки. Равнодействующая от треугольной нагрузки равна площади треугольника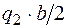 
и приложена в центре тяжести треугольника, поэтому плечо этой равнодействующей относительно точки А равно 
, а относительно точки В – 
. Из этих уравнений найдем RA = – 31,9 кН, RB = – 18,1 кН. Отрицательные знаки показывают, что обе реакции направлены не вверх, как показано на рис. 4.7, а, а в противоположную сторону. Для проверки опорных реакций составим уравнение равновесия "сумма проекций сил на вертикальную ось z равна нулю":
; 
.
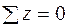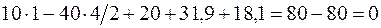Определение внутренних усилий производим, записывая выражения для Q и М в таблицу (табл. 2).
Поясним выражения для Q и М на втором участке, а именно третьи слагаемые в этих выражениях, учитывающие треугольную нагрузку. Чтобы найти равнодействующую от треугольной нагрузки, расположенной слева от рассматриваемого сечения на участке длиной х 2, определим интенсивность распределенной нагрузки в сечении х 2, которая на рис. 4.7, а обозначена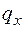 
. Для этого составим пропорцию: 
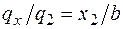, откуда 
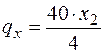. Тогда равнодействующая этой распределенной нагрузки на участке длиной х 2 
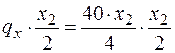. Она приложена в центре тяжести треугольника, и изгибающий момент, создаваемый этой нагрузкой, равен 
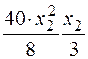, где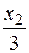 
– плечо равнодействующей.
Таблица 2
 |
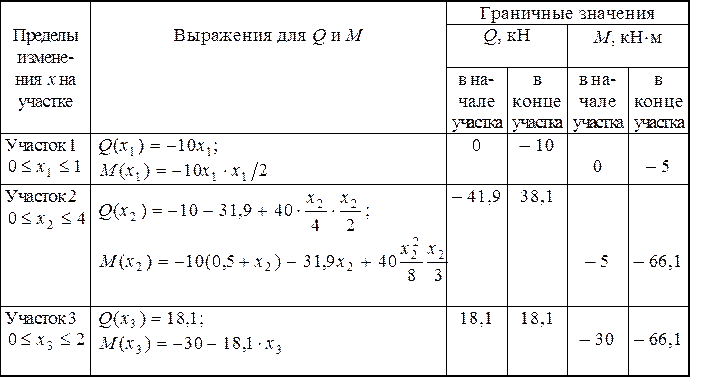Поскольку поперечная сила на втором участке меняет знак, найдем экстремальное значение изгибающего момента в сечении х 0на этом участке (рис. 4.7, б). Определим величину х 0, приравняв выражение для поперечной силы на втором участке нулю:
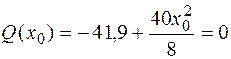, откуда х 0 = 2,89 м. Тогда
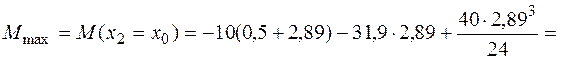
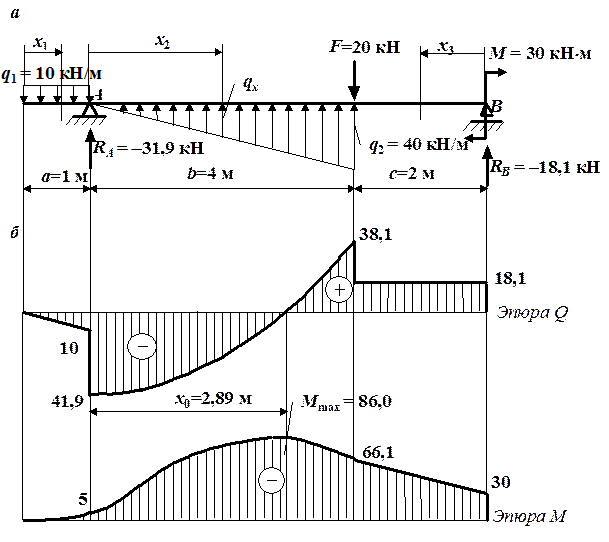 Рис. 4.7. К решению примера 2 по построению эпюр Q и М: а – схема балки с нагрузками; б – эпюры поперечной силы и изгибающего момента |
По полученным в таблице выражениям строим эпюры внутренних усилий. Напомним, что выпуклость эпюры М направлена в сторону распределенной нагрузки. Выпуклость эпюры Q на втором участке можно определить по знаку второй производной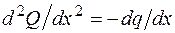 
. В данном случае функция 
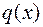является убывающей, следовательно 
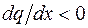, а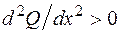 
. Это означает, что эпюра Q имеет выпуклость вниз. Можно определить выпуклость эпюры поперечной силы и по-другому. В сечении, где интенсивность распределенной нагрузки равна нулю (начало второго участка в данной задаче), угол наклона касательной к кривой Q (x) должен равняться нулю, так как в этом сечении 
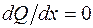. Это возможно тогда, когда функция Q (x) имеет выпуклость вниз.
После того, как Вы нарисовали эпюры, рекомендуем обязательно проанализировать их по правилам проверки правильности построения эпюр.
