Дана разомкнутая система, состоящая из двух апериодических звеньев первого порядка. Представим частотную передаточную функцию данной системы в следующем виде:
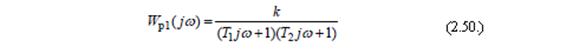
В случае, если Т1 = 0, АФЧХ системы примет вид, представленный на рисунке 73а, в случае, если Т 1 ≠ 0, то АФЧХ системы примет вид, представленный на рисунке 73б. Анализируя графики можно заметить, что АФЧХ разомкнутой системы с передаточной функцией Wр 1(jω) при любых T1 и T2 не будет пересекать отрицательную полуось абсцисс, и такая система всегда будет устойчивой
.
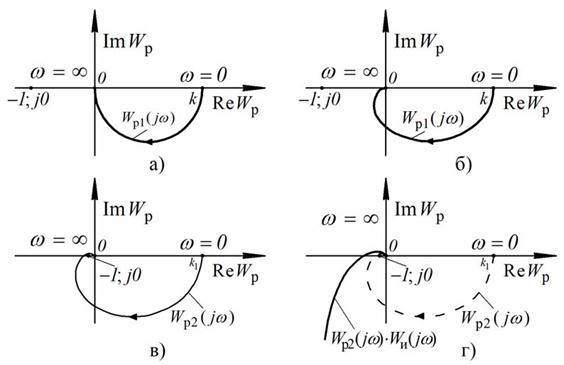
Рис.73. Частотные характеристики разомкнутой САУ
В случае, если формула передаточной функции будет выражена следующим образом:
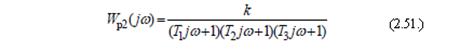
то при различных значениях T 1, T 2 и T 3 система может потерять устойчивость, т.к. АФЧХ системы при изменении T i может охватить точку (-1; j0), как представлено на рисунке 73в.
Снижение степени устойчивости системы достигается включением в разомкнутую цепь интегрирующего звена. Это приведет также к увеличению склонности системы к колебаниям.
В указанном случае АФЧХ системы приблизится к точке (-1; j0), как показано на рисунке 73г, т.к. последовательное включение интегрирующего звена с передаточной функцией Wи(jω) = kи /(jω) приведет к умножению вектора АФЧХ, представленного передаточной функцией Wр2(jω), на вектор Wи(jω) = − j(kи / ω) с аргументом, равным −π/ 2, что будет означать поворот всех векторов Wр2(jω) на угол −π/ 2 с одновременным делением на ω.
С помощью критерия Найквиста также можно определить устойчивость САУ по ЛФЧХ разомкнутой системы. Это возможно благодаря простоте графической интерпретации данной характеристики. Согласно критерию Найквиста выразим условия, при которых замкнутая система будет находиться на границе устойчивости:
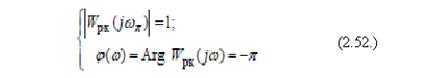
Анализируя данную систему можно сформулировать критерий Найквиста следующим образом – при наличии устойчивой разомкнутой системы, устойчивость системы в замкнутом состоянии должна быть такой, чтобы при достижении ФЧХ разомкнутой системы значения −π, ЛАЧХ этой же системы была отрицательной.
При условии, что ЛФЧХ системы некоторое количество раз пересечет уровень −π до определенной частоты ωс, то система будет устойчивой, если число пересечений будет четным.
На рисунке 75 представлены частотные логарифмические характеристики системы с ЛФЧХ, пересекающей уровень −π несколько раз.
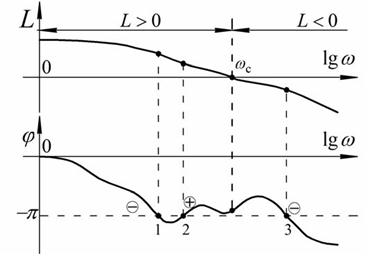
Рис.75. ЛФЧХ системы, пересекающая уровень −π несколько раз.
 2015-01-30
2015-01-30 3800
3800
