Определение интервальных оценок параметров

В инженерной практике нередко возникает вопрос о точности и надежности оценки. Для ответа на этот вопрос поль­зуются такими понятиями, как доверительный интервал и доверительная вероятность.

Под доверительным интервалом понимают диапазон значений, в который с заданной вероятностью попадает истинное значение параметра. Указанную вероятность называют довери­тельной.

Если мы найдем доверительный интервал, то тем самым укажем интервальную оценку параметра. Покажем, как это де­лать, на примере математического ожидания параметра.

Пусть получена точечная оценка математического ожидания пара­метра х.

Обозначим эту оценку как (х).

Доверительный интервал строят обычно симметричным относительно точечной оценки как показано на рис.2.5.

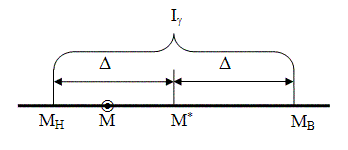
Рис. 2.5. К определению интервальной оценки

Здесь приняты следующие обозначения:

— точечная оценка математического ожидания рас­сматриваемого параметра; для простоты записи знак х опущен;

— истинное значение математического ожидания;

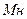— нижняя граница доверительного интервала;

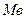— верхняя граница доверительного интервала;

— доверительный интервал;

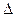— расстояние от точечной оценки до границ дове­рительного интервала.

Дoверительный интервал 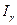обычно выражают как

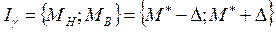. (2.22)

Если мы его найдем, то тем самым укажем интервальную оценку для математического ожидания. Для определения доверительного интервала I, надо знать значение D. Для ее нахождения воспользуемся следующим приемом.

Из теории вероятностей известно, что даже при числе на­блюдений n, стремящимся к 10-15, закон распределения оцен­ки М* (х) близок к нормальному.

Рис. 2.6. Плотность распределения оценки математического ожидания.

Предельными отклонения­ми оценки математического ожидания будем считать точки, отстоящие от рассчи­танной точечной оценки 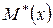на значени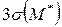е ± , где 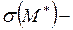среднее квадратичное отклонение оценки математического ожидания.

Поэтому можно записать

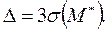
Известно, что для 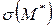справедливо выражение:

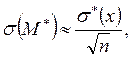(2.23)

где 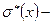точечная оценка среднего квадратичного отклоне­ния рассматриваемого параметра х.

Заменив в выражении (2.23) 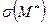ее оценкой, получим

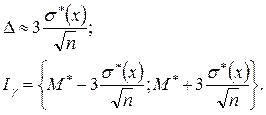(2.24)

Так как мы воспользовались "правилом трех сигм", то значение 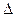, а следовательно и доверительный интервал гаран­тируются с вероятностью 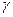= 0,9973. В инженерной практике мо­гут использоваться и другие значения вероятности 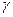, а именно: g = 0,9, g = 0,95, g = 0,99. Поэтому в общем виде 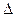может быть представле­на как

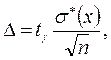(2.25)

где 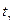- коэффициент, зависящий от доверительной вероятности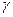

Значение коэффициента t_y в зависимости от вероятности 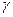Таблица 2.2

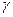	0,8	0,85	0,9	0,95	0,99	0,9973	0,999
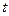	1,282	1,439	1.643	1,960	2,576	3.000	3.290

Этот коэффициент показывает, какое количество величин 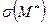— 1,2; 1,6; 2 и т.д. — надо отложить влево и вправо от точечной оценки 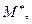чтобы вероятность попадания истинного значения математического ожидания в полученный диапазон бы­ла равна вероятности 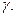В общем случае коэффициент 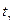. определя­ется как

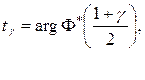(2.26)

где 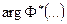—аргумент стандартной функции 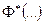нормально­го распределения, для которого сама функция Ф*(...) принимает значения, указанные в скобках.

Например, если Ф*(1,64) = 0.95, то argФ*(0.95) = 1.64.

В окончательном виде искомый доверительный интервал 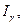а следовательно интервальная оценка математического ожидания, может быть записана в виде

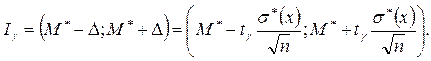(2.27)

Пример2.1. Испытывались на стойкость 2 партии сверл, исходная величина партии 20 штук. К окончанию испытаний (часть сверл были сломаны в процессе испытаний) получены следующие результаты:

Номер партии
Количество сверл
Выборочное среднее, мин
Выборочная ср. кв. откл.		7,5

Зададимся 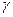= 0,95, т.к. не известен закон распределения то с использованием таблиц для критерия Стьюдента, при числе степеней свободы f₁ = 14 – 1 = 13 и f₂ = 16 - 1 = 15, найдем t_кр1 = 2,16; и t_кр2 = 2,13.

Следовательно, 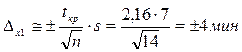, следовательно

23 < М(х) = 27 < 31 мин. Аналогично, ∆_х2 = 3,9 мин, тогда 11,1 < М(х) <18,9.